Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

a) Ta có : x - 4 chia hết cho x + 1
=> x + 1 - 5 chia hết cho x + 1
=> 5 chia hết cho x + 1
=> x + 1 thuộc Ư(5) = {-5;-1;1;5}
=> x = {-6;-2;0;4}
b) 3x - 1 chia hết cho x - 4
=> 3x - 12 + 11 chia hết cho x - 4
=> 3(x - 4) + 11 chia hết cho x - 4
=> 11 chia hết cho x - 4
=> x - 4 thuộc Ư(11) = {-11;-1;1;11}
=> x = {-7;3;5;15}
a,x-4 chia hết cho x+1
\(\Rightarrow\)x-(1+3) chia hết cho x+1
Mà x+1 chia hết cho x+1 nên 3 chia hết cho x+1
\(\Rightarrow\)x thuộc Ư(3)={1;3}
\(\Rightarrow\)x thuộc {0;2}

Câu 2:
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=2\\3^7\cdot a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{1093}\\b\simeq2\end{matrix}\right.\)
Câu 3:
a: \(f\left(x\right)=4x^2+3x+1-3x^2+2x+3=x^2+5x+4\)
b: f(-4)=16-20+4=0
=>x=-4 là nghiệm
c: Đặt f(x)=0
=>(x+4)(x+1)=0
=>x=-4 hoặc x=-1

Bài 1:
a) \(-5\left(x^2-3x+1\right)+x\left(1+5x\right)=x-2\)
\(\Rightarrow-5x^2+15x-5+x+5x^2=x-2\)
\(\Rightarrow16x-5=x-2\)
\(\Rightarrow16x-x=5-2\)
\(\Rightarrow15x=3\)
\(\Rightarrow x=\dfrac{15}{3}=5\)
b) \(12x^2-4x\left(3x+5\right)=10x-17\)
\(\Rightarrow12x^2-12x^2-20x=10x-17\)
\(\Rightarrow-20x=10x-17\)
\(\Rightarrow-20x-10x=-17\)
\(\Rightarrow-30x=-17\)
\(\Rightarrow x=\dfrac{-30}{-17}=\dfrac{30}{17}\)
c) \(-4x\left(x-5\right)+7x\left(x-4\right)-3x^2=12\)
\(\Rightarrow-4x^2+20x+7x^2-28x-3x^2=12\)
\(\Rightarrow-8x=12\)
\(\Rightarrow x=\dfrac{12}{-8}=-\dfrac{4}{3}\)
Bài 2:
a) \(\left(x+5\right)\left(x-7\right)-7x\left(x-3\right)\)
\(=x^2-7x+5x-35-7x^2+21x\)
\(=-6x^2+19x-35\)
b) \(x\left(x^2-x-2\right)-\left(x-5\right)\left(x+1\right)\)
\(=x^3-x^2-2x-x^2+x-5x-5\)
\(=x^3-2x^2-6x-5\)
c) \(\left(x-5\right)\left(x-7\right)-\left(x+4\right)\left(x-3\right)\)
\(=x^2-7x-5x+35-x^2-3x+4x-12\)
\(=11x+23\)
d) \(\left(x-1\right)\left(x-2\right)-\left(x+5\right)\left(x+2\right)\)
\(=x^2-2x-x+2-x^2+2x+5x+10\)
\(=4x+12\)


Bài 1:
a: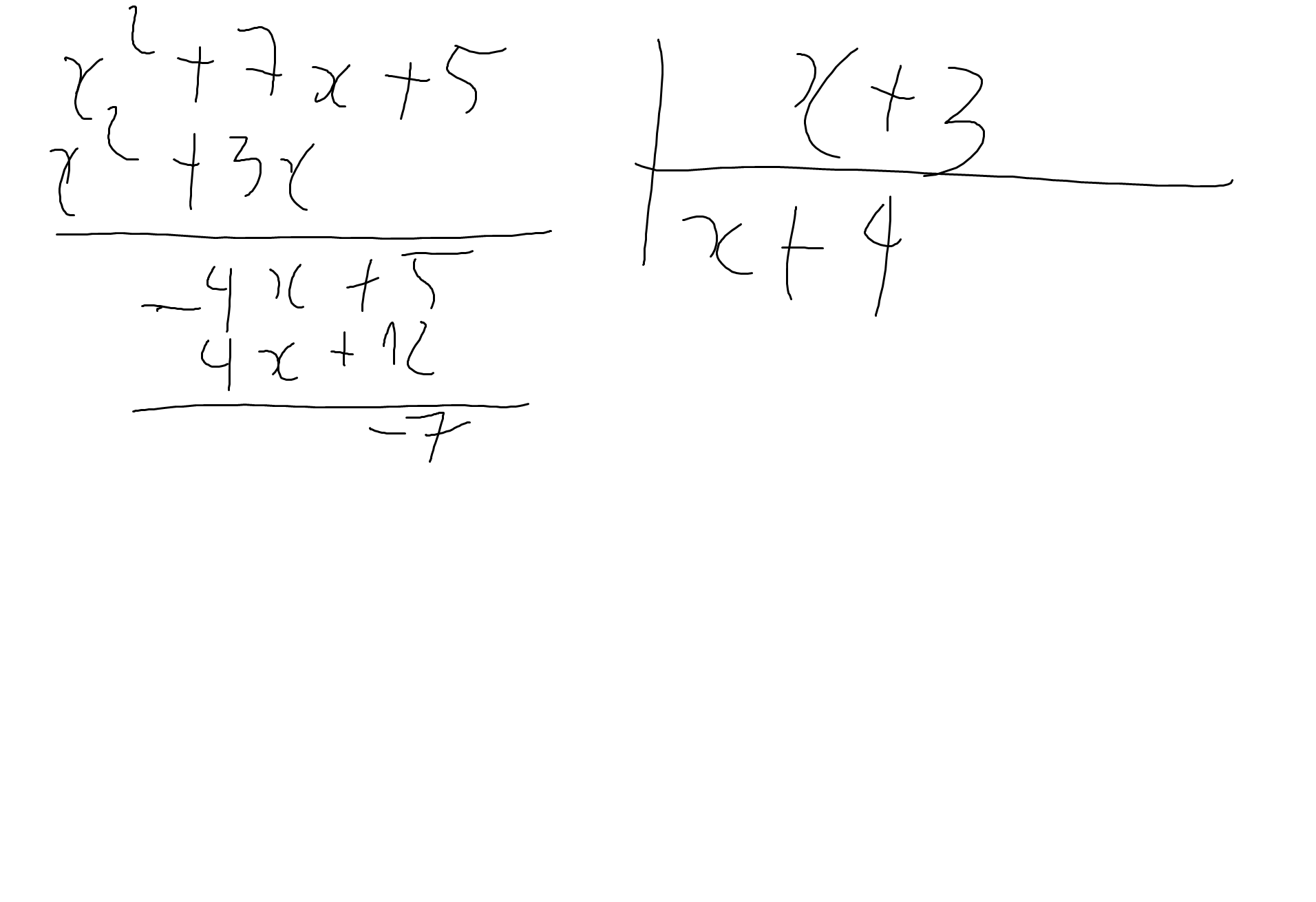
b:
c:
d:
Bài 2:
a: Để \(x^2+4x+a⋮x-2\) thì \(x^2-2x+6x-12+a+12⋮x-2\)
=>a+12=0
=>a=-12
b: \(3x^2+7x+a⋮3x+1\)
=>\(3x^2+x+6x+2+a-2⋮3x+1\)
=>a-2=0