Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Hướng dẫn:
Chọn chiều chuyển động của viên bi thủy tinh là chiều dương.
Trước va chạm: p 0 = m 1 v 1
Sau va chạm: p = m 1 v ' 1 + m 2 v ' 2
Áp dụng định luật bảo toàn động lượng: p = p 0
Suy ra: m 1 v ' 1 + m 2 v ' 2 = m 1 v 1

Dấu trừ chứng tỏ viên bi chuyển động ngược chiều ban đầu.

Giải:
a. Để viên bị đạt được vận tốc v 1 = 3 m / s .
Áp dụng công thức v 1 = v 0 + a t ⇒ t = v 1 − v 0 a = 2 − 0 1 = 2 ( s )
b. Ta có v 2 = 4 m / s mà v 2 – v 0 2 = 2 . a . S
⇒ S = v 2 2 – v 0 2 2. a = 4 2 − 0 2.1 = 16 m
Áp dụng công thức v 2 = v 0 + a t 2 ⇒ t 2 = v 2 − v 0 a = 4 − 0 1 = 4 s

a) Phương trình tọa độ: * Bi A: x 1 = 0 , 1 t 2 (m).
* Bi B: x 2 = 1 − t + 0 , 1 t 2 (m).
b) Khi lăn đến B, tọa độ của bi A là x 1 = 1 m. Ta có: 0 , 1 t 2 = 1 ⇒ t = 10 s.
Nếu coi mặt phẳng nghiêng là đủ dài để bi 2 chuyển động thì quãng đường dài nhất mà 2 bi có thể lăn được cho đến khi dừng v = 0 :
Từ công thức v 2 − v 0 2 = 2 a s ⇒ s m a x = v 2 − v 0 2 2 a = 0 − 1 2 2.0 , 2 = − 2.5 m.
Ta thấy s m a x > A B nên bi 2 có thể lên đỉnh mặt nghiêng.
c) Khi hai hòn bi gặp nhau thì x 1 = x 2 ⇔ 0 , 1 t 2 = 1 − t + 0 , 1 t 2 ⇒ t = 1 s.
Tọa độ gặp nhau: x 1 = x 2 = 0 , 1.1 2 = 0 , 1 m.

Sử dụng định luật bảo toàn động lượng và bảo toàn cơ năng cho va chạm giữa hai vật, ta thu được kết quả sau:
a/ v 2 = m 1 v 1 m 2 = 4.3 , 2 6 = 2 , 13 m / s
b/ v = m 1 ( v 1 + v 1 / ) m 2 = 4 ( 3 , 2 + 3 ) 6 = 4 , 13 m / s

Chọn mốc thế năng ở chân dốc
a. Gọi A là đỉnh dốc, B là giữa dốc. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ⇒ v B = 2.10 ( 0 , 4 − 0 , 2 ) = 2 ( m / s )
b. Gọi C ở chân dốc. Theo định luật bảo toàn cơ năng
W A = W C ⇒ m g z A = 1 2 m v C 2 ⇒ v C = 2 g z A = 2.10.0 , 4 = 2 2 ( m / s )
c.Gọi D là vị trí trên dốc để thế năng của viên bi bằng 3 lần động năng. Theo định luật bảo toàn cơ năng
W A = W D ⇒ m g z A = W d + W t = 4 3 W t ⇒ m g z A = 4 3 m g z D ⇒ z D = 3 4 z A = 3 4 .0 , 4 = 0 , 3 ( m )
Theo bài ra
W t = 3 W ⇒ m g z D = 3 1 2 m v D 2 ⇒ v D = 2. g . z A 3 = 2.10.0 , 3 3 = 2 ( m / s )

Chọn chiều dương là chiều chuyển động của viên bi một trước lúc va chạm
Theo định luật bảo toàn động lượng
m 1 . v → 1 + m 2 . v → 2 = m 1 . v → 1 ' + m 2 . v → 2 '
a. Sau va chạm hai viên bi đứng yên nên
v 1 ' = v 2 ' = 0 ( m / s )
Chiếu lên chiều dương ta có
m 1 . v 1 − m 2 . v 2 = 0 ⇒ v 2 = m 1 . v 1 m 2 = 4.4 8 = 2 ( m / s )
b. Sau va chạm viên bi hai đứng yên viên bi một chuyển động ngược chiều với vận tốc 3 m/s ta có:
Chiếu lên chiều dương
m 1 . v 1 − m 2 . v 2 = − m 1 . v 1 / + 0 ⇒ v 2 = m 1 . v 1 + m 1 . v 1 / m 2 ⇒ v 2 = 4.4 + 4.3 8 = 3 , 5 ( m / s )

Chọn chiều dương là chiều chuyển động của bi
a) Từ công thức tính quãng đường: \(s=\frac{at^2}{2}\)
Quãng đường đi được trong 4s đầu tiên: \(s_4=\frac{\text{a4}^2}{2}=8a\)
Quãng đường đi được trong 5s đầu tiên
\(s_5=\frac{\text{a5}^2}{2}=12,5a\)
Quãng đường đi được trong giây thứ 5:
\(\Delta s=s_5-s_4=12,5a-8a=4,5a\)
Ta có: \(\Delta s=0,36m\Rightarrow a=\frac{0,36}{4,5}=0,08\) m/s2
b) Với a = 0,08m/s2 có 5s = 12,5a = 12,5 . 0,08 = 1m
Từ công thức v = at => Vận tốc ở cuổi quãng đường v = 0,8.5 = 0,4 m/s
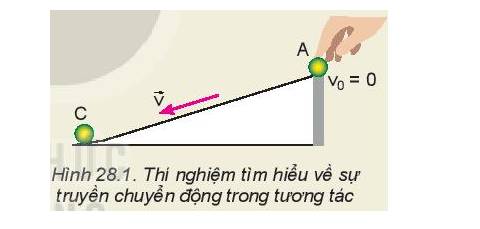


- Trong thí nghiệm 1, vận tốc của viên A và viên bi B khi đến chân dốc không giống nhau. Vận tốc và khối lượng của viên bi B đều lớn hơn vận tốc và khối lượng của viên bi A nên viên bi B đẩy viên bi C lăn xa hơn
- Trong thí nghiệm 2, ứng với độ dốc sau khi tăng độ dốc của máng trượt lên thì vận tốc của viên A lớn hơn khi va chạm với viên bi C. Sau khi tăng độ dốc thì thì viên C lăn xa hơn