
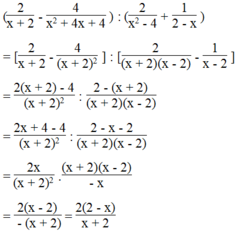
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

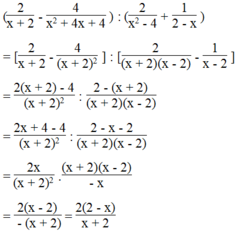

\(ĐKXĐ:x\ne\pm2\)
\(\left(\frac{2}{x+2}-\frac{4}{x^2+4x+4}\right):\left(\frac{2}{x^2-4}+\frac{1}{2-x}\right)\)
\(=\left[\frac{2}{x+2}-\frac{4}{\left(x+2\right)^2}\right]:\left[\frac{2}{\left(x-2\right)\left(x+2\right)}+\frac{-1}{x-2}\right]\)
\(=\left[\frac{2\left(x+2\right)}{\left(x+2\right)^2}-\frac{4}{\left(x+2\right)^2}\right]:\left[\frac{2}{\left(x-2\right)\left(x+2\right)}+\frac{-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\frac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\frac{2-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)\(=\frac{2x+4-4}{\left(x+2\right)^2}:\frac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{2x}{\left(x+2\right)^2}:\frac{-x}{\left(x-2\right)\left(x+2\right)}=\frac{2x}{\left(x+2\right)^2}.\frac{-\left(x-2\right)\left(x+2\right)}{x}\)
\(=\frac{-2\left(x-2\right)}{x+2}\)
\(\left(\frac{2}{x+2}-\frac{4}{x^2+4x+4}\right):\left(\frac{2}{x^2-4}+\frac{1}{2-x}\right)\)
\(\Leftrightarrow\left(\frac{2}{x+2}-\frac{4}{\left(x+2\right)^2}\right):\left(\frac{2}{\left(x-2\right)\left(x+2\right)}+\frac{1}{2-x}\right)\)
\(\Leftrightarrow\frac{2x+4-4}{\left(x+2\right)^2}:\frac{2+x+2}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\frac{2x}{\left(x+2\right)^2}\cdot\frac{\left(x-2\right)\left(x+2\right)}{x+4}\)
\(\Leftrightarrow\frac{2x^2-4x}{\left(x+2\right)\left(x+4\right)}\)

Ta có \(\left(\frac{1}{x^2+4x+4}-\frac{1}{x^2-4x+4}\right):\left(\frac{1}{x+2}+\frac{1}{x-2}\right)\)
\(=\frac{\left(x-2\right)^2-\left(x+2\right)^2}{\left(x-2\right)^2\left(x+2\right)^2}:\frac{x-2+x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{\left(x-2+x+2\right)\left(x-2-x-2\right)}{\left(x-2\right)^2\left(x+2\right)^2}:\frac{2x}{\left(x+2\right)\left(x-2\right)}\)
\(\frac{-4.2x}{\left(x+2\right)^2\left(x-2\right)^2}.\frac{\left(x+2\right)\left(x-2\right)}{2x}=\frac{-4}{\left(x+2\right)\left(x-2\right)}\)

\(a,\frac{x}{2\left(x-3\right)}+\frac{x}{2\left(x+1\right)}=\frac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\frac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\frac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\frac{4x}{2\left(x+1\right)\left(x-3\right)}\)
\(x\left(x+1\right)+x\left(x-3\right)=4x\)
\(x^2+x+x^2-3x=4x\)
\(2x^2-2x=4x\)
\(2x^2-2x-4x=0\)
\(2x\left(x-3\right)=0\)
\(2x=0\Leftrightarrow x=0\)
hoặc
\(x-3=0\Leftrightarrow x=3\)
b) \(ĐKXĐ:x\ne\pm4\)
\(5+\frac{96}{x^2-16}=\frac{2x-1}{x+4}-\frac{3x-1}{4-x}\)
\(\Leftrightarrow5+\frac{96}{x^2-16}=\frac{2x-1}{x+4}+\frac{3x-1}{x-4}\)
\(\Leftrightarrow\frac{5\left(x^2-16\right)}{x^2-16}+\frac{96}{x^2-16}=\frac{\left(2x-1\right)\left(x-4\right)}{x^2-16}+\frac{\left(3x-1\right)\left(x+4\right)}{x^2-16}\)
\(\Rightarrow5\left(x^2-16\right)+96=\left(2x-1\right)\left(x-4\right)+\left(3x-1\right)\left(x+4\right)\)
\(\Leftrightarrow5x^2-80+96=2x^2-9x+4+3x^2+11x-4\)
\(\Leftrightarrow5x^2-2x^2-3x^2+9x-11x=4-4+80-96\)
\(\Leftrightarrow-2x=-16\)\(\Leftrightarrow x=8\)( thoả mãn ĐKXĐ )
Vậy tập nghiệm của phương trình là: \(S=\left\{8\right\}\)

\(1.\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)\)
\(=\sqrt{x}\left(\sqrt{x}-2\right)+1\left(\sqrt{x}-2\right)\)
\(=x-2\sqrt{x}+\sqrt{x}-2\)
\(=x-\sqrt{x}-2\)
\(2.\left(x+4\right)\left(x-2\right)-\left(x-3\right)^2\)
\(=x\left(x-2\right)+4\left(x-2\right)-\left(x^2-6x+9\right)\)
\(=x^2-2x+4x-8-x^2+6x-9\)
\(=8x-17\)

a) \(\frac{3x}{2x+4}+\frac{x+3}{x^2-4}\)
\(=\frac{3x}{2\left(x+2\right)}+\frac{x+3}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{3x\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}+\frac{2\left(x+3\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{3x\left(x-2\right)+2\left(x+3\right)}{2\left(x+2\right)\left(x-2\right)}\)
\(=\frac{3x^2-6x+2x+6}{2\left(x^2-4\right)}\)
\(=\frac{3x^2-4x+6}{2\left(x^2-4\right)}\)

ĐKx\(\ne\)2,x\(\ne\)0
\(=\)\(\frac{2(x+2)+2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\):\(\frac{4x}{\left(x+2\right)^2}\)
=\(\frac{2x+4+2x-4}{\left(x-2\right)\left(x+2\right)}\)\(\frac{(x+2)^2}{4x}\)
=\(\frac{x+2}{x-2}\)
\(\left(\frac{2}{x-2}+\frac{2}{x+2}\right):\frac{4x}{x^2+4x+4}\)
\(=\left(\frac{2}{x-2}+\frac{2}{x+2}\right):\frac{4x}{\left(x+2\right)^2}\)
\(=\left(\frac{2}{x-2}+\frac{2}{x+2}\right).\frac{\left(x+2\right)^2}{4x}\)
\(=\frac{4x}{x^2-4}.\frac{\left(x+2\right)^2}{4x}\)
\(=\frac{4x.\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right).4}\)
\(=\frac{x+2}{x-2}\)

\(\frac{3\left(x+1\right)}{x+2}-\frac{3x-6}{x^2-4}\)
\(=\frac{3\left(x+1\right)}{x+2}-\left(\frac{3x-6}{x^2-4}\right)\)
\(=\frac{3x^2-6x^2-12x+24}{x^3+2x^2-4x-8}\)
\(=\frac{3\left(x+2\right)\left(x-2\right)\left(x-2\right)}{\left(x+2\right)\left(x+2\right)\left(x-2\right)}\)
\(=\frac{3x-6}{x+2}\)
\(\frac{x^2+4x+4}{1-x}.\frac{\left(1-x\right)^2}{3\left(x+2\right)^3}\)
\(=\frac{x^2+4x+4}{1-x}.\left[\frac{\left(1-x\right)^2}{3\left(x+2\right)^3}\right]\)
\(=\frac{x^4+2x^3-3x^2-4x+4}{-3x^4-15x^3-18x^2+12x+24}\)
\(=\frac{\left(x-1\right)\left(x-1\right)\left(x+2\right)\left(x+2\right)}{3\left(-x+1\right)\left(x+2\right)\left(x+2\right)\left(x+2\right)}\)
\(=\frac{-x+1}{3x+6}\)

a) \(\dfrac{15x}{7y^3}.\dfrac{2y^2}{x^2}=\dfrac{15x.2y^2}{7y^3.x^2}=\dfrac{30}{7xy}\)
b) \(\dfrac{4y^2}{11x^4}.\left(-\dfrac{3x^2}{8y}\right)=\dfrac{-4y^2.3x^2}{11x^4.8y}=\dfrac{-3y}{22x^2}\)
c) \(\dfrac{x^3-8}{5x+20}.\dfrac{x^2+4x}{x^2+2x+4}\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{5\left(x+4\right)}.\dfrac{x\left(x+4\right)}{x^2+2x+4}\\ =\dfrac{x^2-2x}{5}\)