Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HÌNH CHỈ MANG TÍNH MINH HỌA
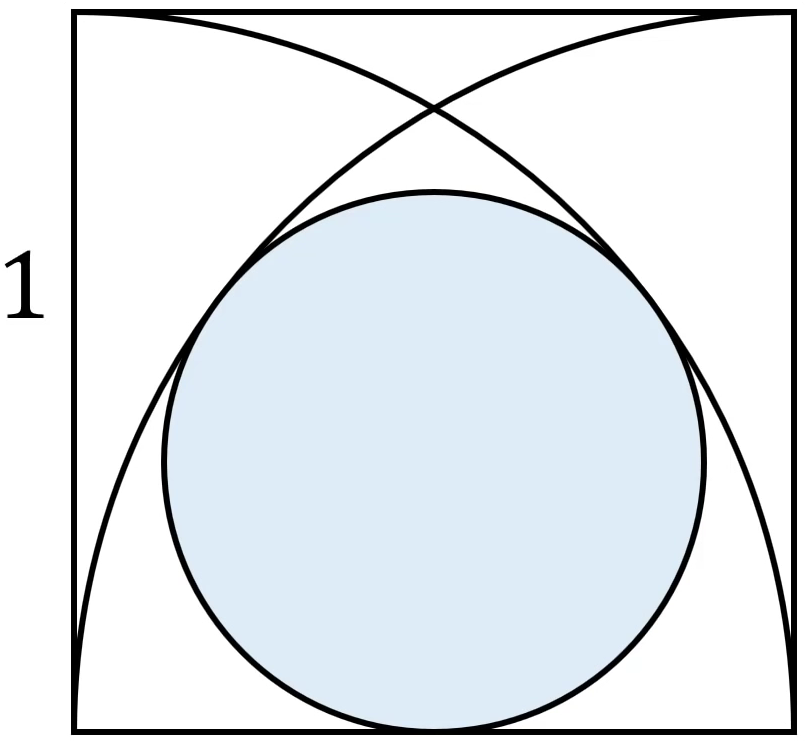
TA CÓ DIỆN TÍCH CỦA 4 NỬA ĐƯỜNG TRÒN CÓ ĐƯỜNG KÍNH LÀ CẠNH HÌNH VUÔNG LÀ
\(\left(\frac{\sqrt[]{6}-\sqrt{2}}{2\sqrt{2}+12\sqrt{5}}\right)^2.\pi\)
TA DỄ DÀNG NHẬN THẤY TỔNG DIỆN TÍCH CỦA 4 NỬA ĐƯỜNG TRÒN BẰNG TỔNG DIỆN TÍCH HÌNH VUÔNG CONNGJ VỚI DIỆN TÍCH HÌNH HOA THỊ
=> DIỆN TÍCH HOA THỊ = \(\left(\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}+6\sqrt{5}}\right)^2.\pi-\left(\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}+6\sqrt{5}}\right)^2=\left(\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}+6\sqrt{2}}\right)^2\left(\pi-1\right)\)
= \(\left(\frac{8-2\sqrt{12}}{182+12\sqrt{10}}\right)\left(\pi-1\right)\)

Chu vi của hình vuông là:
\(\sqrt{14\cdot5.3}\cdot4=34,46\left(cm\right)\)
Ta có:
Áp dụng định lý Pi-ta-go, ta có công thức để tìm đường chéo hình vuông\(=a\sqrt{2}\)
\(\Rightarrow\)Cứ sau một lần như thế thì cạnh hình vuông sẽ tăng lên \(\sqrt{2}\)hay diện tích hình vuông sau 1 lần như thế thì sẽ gấp\(\sqrt{2}^2=4lần\)
\(\Rightarrow\)Cứ một lần hình vuông bằng cạnh hình vuông trước thì diện tích sẽ gấp 4 lần:
\(\Rightarrow\)Nếu diện tích hình vuông thứ 2022 hay lặp lại cái trên 2022 lần thì diện tích sẽ gấp \(2022\cdot4=8088lần\)hình vuông ban đầu.
Gọi diện tích các hình vuông là S1 ; S2 ; ... S2022 với độ dài cạnh tương ứng là a ; a2 ; a3 ; ... ; a2022
Dựng hình vuông thứ n có cạnh an với độ dài cạnh là đường chéo hình vuông có cạnh an - 1 (n \(\inℕ^∗\) )
=> Sn = (an)2 (1)
Sn - 1 = (an-1)2 (2)
Khi đó (an)2= 2(an - 1)2
=> \(a_n=\sqrt{2}a_{n-1}\)(3)
Từ (3)(2)(1) => \(S_n=2.S_{n-1}\)
Khi đó với 1 < n < 2023
=> \(S_{2022}=2S_{2021}=2^2S_{2020}=...=2^{2021}S_1\)= 22021a2