Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các giá trị khác nhau của dấu hiệu là: 8,2; 8,5; 8,6; 9,0; 9,1; 9,2
Vậy có 6 giá trị khác nhau của dấu hiệu
Chọn đáp án B

Quan sát bảng ta thấy tần số tương ứng của giá trị 8,5 là 3
Chọn đáp án C

Tần số tương ứng với các giá trị 8,2; 8,5; 8,6; 9,0 là 1; 3; 1; 2
Vậy giá trị có tần số lớn nhất là 8,5
Chọn đáp án B

a) Số học sinh giỏi toàn diện trong nhóm là:
20 x 3/5 = 12 ( học sinh)
b) Số học sinh của lớp 7A là:
12 : 2/7 = 42 ( học sinh)
* LƯU Ý: Mik thay đổi đề một chút, bởi vì số học sinh của lớp 7A phải bằng 7/2 số học sinh toàn diện.

Gọi số học sinh lớp \(7A;7B;7C\) lần lượt là \(a;b;c\)
Theo đề bài ta có:
\(\dfrac{2}{3}a=\dfrac{3}{4}b=\dfrac{4}{5}c\Leftrightarrow\dfrac{2a}{3}=\dfrac{3b}{4}=\dfrac{4c}{5}\)
Tương đương với:
\(\dfrac{2a}{3}.\dfrac{1}{12}=\dfrac{3b}{4}.\dfrac{1}{12}=\dfrac{4c}{5}.\dfrac{1}{12}\)
\(\Leftrightarrow\dfrac{2a}{36}=\dfrac{3b}{48}=\dfrac{4c}{60}\)
\(\Leftrightarrow\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}=\dfrac{a+b-c}{18+16-15}=\dfrac{57}{19}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=18.3=54\\b=16.3=48\\c=15.3=45\end{matrix}\right.\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{4}{3}}=\dfrac{b}{\dfrac{7}{6}}=\dfrac{c}{\dfrac{3}{2}}=\dfrac{a+b+c}{\dfrac{4}{3}+\dfrac{7}{6}+\dfrac{3}{2}}=\dfrac{144}{4}=36\)
Do đó: a=48; b=42; c=54

1/ Ta cần c/m \(3^{n+1}\left(3^2+1\right)+2^{n+2}\left(2+1\right)⋮6\)
Tức là \(3^{n+1}.10+2^{n+2}.3⋮6\) (1)
Ta có:
Với n = 0 \(3^{n+1}.10+2^{n+2}.3=114⋮6\Rightarrow\)mệnh đề đúng với n = 0 (1)
Giả sử điều đó đúng với n = k.Tức là \(3^{k+1}.10+2^{k+2}.3⋮6\) (2)
Ta sẽ c/m nó đúng với n = k + 1.
Thật vậy,ta cần c/m: \(3^{k+2}.10+2^{k+3}.3⋮6\)
\(\Leftrightarrow3^k.90+2^k.24⋮6\)
Điều này luôn đúng do \(90⋮6;24⋮6\rightarrow3^k.90⋮6;2^k.24⋮6\)
\(\Rightarrow3^k.90+2^k.24⋮6\) (3)
Từ (1);(2) và (3) ta được đpcm.
2.b)Gọi số học sinh của 3 lớp lần lượt là x,y,z > 0
Theo đề bài ra,ta có: \(\frac{2x}{3}=\frac{y}{1}=\frac{4z}{5}\) và \(\left(x+y\right)-z=57\)
Ta có: \(\frac{2x}{3}=\frac{y}{1}=\frac{4z}{5}\Leftrightarrow\frac{x}{\frac{3}{2}}=\frac{y}{1}=\frac{z}{\frac{5}{4}}\)
Áp dụng t/c dãy tỉ số "=" nhau,ta có:
\(\frac{x}{\frac{3}{2}}=\frac{y}{1}=\frac{z}{\frac{5}{4}}=\frac{\left(x+y\right)-z}{\left(\frac{3}{2}+1\right)-\frac{5}{4}}=\frac{57}{\frac{5}{4}}=\frac{228}{5}\)
Đến đây bạn tự suy ra,nếu ra số hữu tỉ thì làm tròn nha!
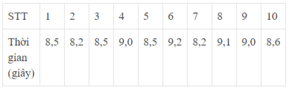
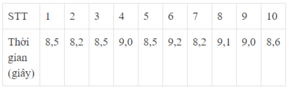

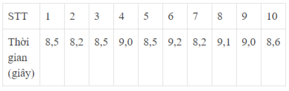
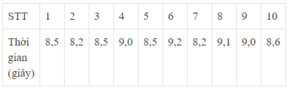
Dấu hiệu ở đây là thời gian chạy 50m của học sinh nhóm 1 lớp 9D
Chọn đáp án B