Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: sử dụng công thức tính khoảng vân , số vân sáng trong miền giao thoa L
Cách giải:
Khoảng vân tương ứng với hai bức xạ lần lượt là:
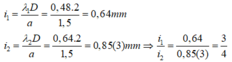
Để tìm số vân sáng trùng nhau ta coi như hệ giao thoa của 1 ánh sáng có khoảng vân là:
![]()
Trong miền giao thoa có bề rộng L = 7,68mm có số vân sáng trùng nhau là:
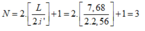
Đáp án C

- Khoảng vân tương ứng với hai bức xạ lần lượt là:
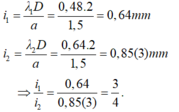
- Để tìm số vân sáng trùng nhau ta coi như hệ giao thoa của 1 ánh sáng có khoảng vân là:
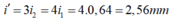
- Trong miền giao thoa có bề rộng L = 7,68mm có số vân sáng trùng nhau là:
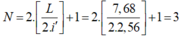

Khoảng cách giữa 2 vân sáng gần nhau nhất cùng màu với vân trung tâm: \(x_T=k_1i_1=k_2i_2\)(1)
\(\Rightarrow k_1\lambda_1=k_2\lambda_2\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,6}{0,48}=\frac{5}{4}\)
\(\Rightarrow\begin{cases}k_1=5\\k_2=4\end{cases}\)
Thay vào (1) \(x_T=5i_1=4i_2\)
Như vậy tại vị trí 2 vân trùng nhau kể từ vân trung tâm có vân bậc 5 của \(\lambda_1\) và bậc 4 của \(\lambda_2\)
Do đó, giữa 2 vân sáng cùng màu vân trung tâm có: 4 vân sáng λ1 và 3 vân sáng λ2.
Đáp án A.

\(i_1=\dfrac{\lambda_1.D}{a}=1,2mm\)
Số vân sáng của i1 là: \(|\dfrac{24}{2.1,2}|.2+1=21\)
Số vân sáng của i2 là: \(33+5-21=17\)
\(\Rightarrow i_1=1,5mm\)
\(\Rightarrow \lambda_2=0,75\mu m\)

\(i_1 = \frac{\lambda_1D_1}{a}\)
\(i_2 = \frac{\lambda_2D_2}{a}\)
=> \(\frac{i_1}{i_2} = \frac{\lambda_1D_1}{\lambda_2D_2} \)
=> \(\frac{\lambda_1}{\lambda_2} = \frac{i_1D_2}{i_2D_1} = \frac{1.2}{3.1}= \frac{2}{3}\) (do \(i_2 = 3i_1; D_2 = 2D_1\))
=> \(\lambda_2 = \frac{3\lambda_1}{2} = \frac{3.0,4}{2} = 0,6 \mu m.\)
Chọn đáp án.A

Khoảng cách giữa 2 vân sáng liên tiếp có màu giống màu vân chính giữa là: \(x_T\)
\(\Rightarrow x_T=k_1.i_1=k_2.i_2\)
\(\Rightarrow k_1.\lambda_1=k_2.\lambda_2\)
\(\Rightarrow\dfrac{k_1}{k_2}=\dfrac{\lambda_2}{\lambda_1}=\dfrac{4}{3}\)
\(\Rightarrow k_1=4;k_2=3\)
\(\Rightarrow 2,56=4.i_1=3.i_2\)
\(\Rightarrow i_1=0,64mm\); \(i_2=0,85mm\)
\(\Rightarrow \lambda_2=\dfrac{1,5.0,85}{2}=0,64\mu m\)

Khoảng cách giữa hai vân sáng cùng màu gần nhất với vân chính giữa là : x = k1 i1 = k2 i2 => k1λ1 = k2λ2
Nhận xét: k2 = 9 => k1.720 = 9 λ2 => λ2 = 80 k1.
Do λ2 có giá trị trong khoảng từ 500nm đến 575nm nên dễ thấy k1 = 7
=> λ2 = 560 nm.
Đáp án D

Giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 8 vân sáng màu lục tức là khoảng cách đó là \(\Delta x _{min}= 9i_{lục}.\)
=> \(9i_{lục}= k_2 i_{đỏ}=> 9\lambda_{lục}= k_2 \lambda_{đỏ}\)
=> \(\lambda_{lục} = \frac{k_2 \lambda_{đỏ}}{9}.\ \ (1)\)
Mà \(500 n m \leq \lambda_{lục} \leq 575nm.\)
Thay (1) vào <=> \(500 n m \leq \frac{k_2 \lambda_{đỏ}}{9} \leq 575nm.\)
<=> \(\frac{500.9}{720} \leq k_2 \leq \frac{575.9}{720}\)
<=> \(6,25 \leq k_2 \leq 7,1875\)
=> \(k_2 = 7=> (1): \lambda_{lục} = 560nm.\)
720nm = 0,72 μm
giữa 2 vân sáng gần nhau nhất và cùng màu vs vân sáng trung tâm có 8 vân sáng màu lục => Tại vị trí trùng đó là VS bậc 9 của λlục
Tại VT trùng nhau: x_kđỏ = x_9lục
<=> kđỏ.λđỏ = 9.λlục
<=> kđỏ/9 = λlục/λđỏ = λ/0,72
=> λ = (0,72.kđỏ)/9 = 0,08.kđỏ (*)
0,5 ≤ λ = 0,08.kđỏ ≤ 0,575 μm
6,25 ≤ kđỏ ≤ 7,1875
=> kđỏ = 7
thế vào (*) λ = 0,56 (μm) = 560nm
đáp án : D

Đáp án C
Khoảng vân tương ứng với hai bức xạ lần lượt là:
Để tìm số vân sáng trùng nhau ta coi như hệ giao thoa của 1 ánh sáng có khoảng vân là:
Trong miền giao thoa có bề rộng L = 7,68mm có số vân sáng trùng nhau là: