
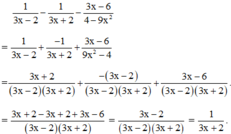
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

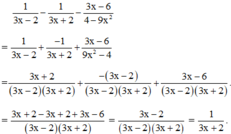

a,ĐKXĐ:\(x\ne2,x\ne-3\)
\(A=\frac{x+2}{x+3}-\frac{5}{x^2+x-6}+\frac{1}{2-x}\)
\(=\frac{x+2}{x+3}-\frac{5}{\left(x-2\right)\left(x+3\right)}-\frac{1}{x-2}\)
\(=\frac{\left(x+2\right)\left(x-2\right)-5-\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}\)
\(=\frac{x^2-4-5-x-3}{\left(x-2\right)\left(x+3\right)}\)
\(=\frac{x^2-x-12}{\left(x-2\right)\left(x+3\right)}\)
\(=\frac{\left(x-4\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}\)
\(=\frac{x-4}{x-2}\)
c,Để A = - 3/4
thì: \(\frac{x-4}{x-2}=-\frac{3}{4}\)
\(\Leftrightarrow4\left(x-4\right)=-3\left(x-2\right)\)
\(4x-16=-3x+6\)
\(4x+3x=6+16\)
\(7x=22\)
\(x=\frac{22}{7}\)
d,\(A=\frac{x-4}{x-2}=\frac{x-2-2}{x-2}=\frac{x-2}{x-2}-\frac{2}{x-2}=1-\frac{2}{x-2}\)
Để A nguyên thì: \(x-2\inƯ\left(2\right)\)
Ta có: \(Ư\left(2\right)=\left\{\pm1,\pm2\right\}\)
Xét từng TH:
_ x - 2 = -1 => x = 1
_ x - 2 = 1 => x = 3
_ x - 2 = -2 => x = 0
_ x- 2 = 2 => x= 4
Vậy: \(x\in\left\{0,1,3,4\right\}\)
=.= hok tốt!!

\(A=\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
a) ĐKXĐ:
\(\begin{cases} x+3\ne 0\\ x^2+x-6 \ne 0 \Rightarrow (x+3)(x-2) \ne 0\\ 2-x\ne 0 \end{cases} \\\Leftrightarrow \begin{cases} x\ne -3\\ x\ne 2 \end{cases} \)
b) Với \(x\ne-3;x\ne2\) ta có:
\(A=\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
\(\Leftrightarrow\dfrac{x+2}{x+3}-\dfrac{5}{\left(x-2\right)\left(x+3\right)}+\dfrac{1}{2-x}\)
\(\Leftrightarrow\dfrac{x+2}{x+3}-\dfrac{5}{\left(x-2\right)\left(x+3\right)}-\dfrac{1}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\dfrac{5}{\left(x-2\right)\left(x+3\right)}-\dfrac{x+3}{\left(x-2\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{x^2-4}{\left(x+3\right)\left(x-2\right)}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x^2-4-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x-4}{x-2}\)

\(e ) Để \) \(M\)\(\in\)\(Z \) \(thì\) \(1 \)\(⋮\)\(x +3\)
\(\Leftrightarrow\)\(x + 3 \)\(\in\)\(Ư\)\((1)\)\(= \) { \(\pm\)\(1 \) }
\(Lập\) \(bảng :\)
| \(x +3\) | \(1\) | \(- 1\) |
| \(x\) | \(-2\) | \(- 4\) |
\(Vậy : Để \) \(M\)\(\in\)\(Z\) \(thì\) \(x\)\(\in\){ \(- 4 ; - 2\) }
e) Để M \(\in\)Z <=> \(\frac{1}{x+3}\in Z\)
<=> 1 \(⋮\)x + 3 <=> x + 3 \(\in\)Ư(1) = {1; -1}
Lập bảng:
| x + 3 | 1 | -1 |
| x | -2 | -4 |
Vậy ....
f) Ta có: M > 0
=> \(\frac{1}{x+3}\) > 0
Do 1 > 0 => x + 3 > 0
=> x > -3
Vậy để M > 0 khi x > -3 ; x \(\ne\)3 và x \(\ne\)-3/2

a, \(Đkxđ:x\ne-3;x\ne2\)
b,\(A=\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
\(=\dfrac{x+2}{x+3}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{1}{x-2}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2-x-12}{\left(x-2\right)\left(x+3\right)}\)\(=\dfrac{x-4}{x-2}\)
c,\(A=-\dfrac{3}{4}\) khi \(\dfrac{x-4}{x-2}=-\dfrac{3}{4}\)
\(\Leftrightarrow\left(x-4\right).4=-3\left(x-2\right)\)
\(\Leftrightarrow4x-16=-3x+6\)
\(\Leftrightarrow7x=22\)
\(\Leftrightarrow x=\dfrac{22}{7}\)
Vậy khi \(x=\dfrac{22}{7}\) thì \(A=-\dfrac{3}{4}\)
a) ĐKXĐ : \(\left\{{}\begin{matrix}x+3\ne0\\2-x\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne2\end{matrix}\right.\)
b) \(A=\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}-\dfrac{1}{x-2}\)
\(A=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}\)
\(A=\dfrac{-x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}=\dfrac{x-4}{x-2}\)
c) Để \(A=\dfrac{-3}{4}\) thì :
\(A=\dfrac{x-4}{x-2}=\dfrac{-3}{4}\)
\(\Rightarrow\dfrac{x-4}{x-2}+\dfrac{3}{4}=0\)
\(\Rightarrow\dfrac{4\left(x-4\right)}{4\left(x-2\right)}+\dfrac{3\left(x-2\right)}{4\left(x-2\right)}=0\)
\(\Rightarrow4x-16+3x-6=0\)
\(\Rightarrow7x+22=0\)
\(\Rightarrow x=\dfrac{-22}{7}\)
d) Ta có : \(A=\dfrac{x-4}{x-2}=\dfrac{x-2-2}{x-2}=1-\dfrac{2}{x-2}\)
Vì \(1\in Z\) để \(A\in Z\) thì \(\dfrac{2}{x-2}\in Z\)
\(\Rightarrow x-2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Có : \(\left\{{}\begin{matrix}x-2=1=>x=3\\x-2=-1=>x=1\\x-2=2=>x=4\\x-2=-2=>0\end{matrix}\right.\)
Vậy để A nhận gt nguyên thì x \(\in\left\{3;1;4;0\right\}\)
e) \(x^2-9=0\)
\(\Rightarrow\left(x+3\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(loại\right)\\x=3\end{matrix}\right.\)
Thay vào A ta có :
\(A=\dfrac{x-4}{x-2}=\dfrac{3-4}{3-2}=-1\)