Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cj định chửi cơ mak nghĩ ở đây cần có sự tế nhị nên thôi chứ k thì cho e đọc cả bài luận đến sáng mai nhé :)

1.1 Hình vuông có tối đa 4 góc vậy 4 hình vuông có tối đa 20 góc. S
2.1 hình vuông có tối đa 4 góc vậy 4 hình vuông có tối đa 16 góc. Đ
3. 1 hình vuông có tối thiểu 4 góc vậy 4 hình vuông có tối thiểu 16 góc. Đ
4.1 hình vuông có tối thiểu 1 góc vậy 4 hình vuông có tối thiểu 16 góc. S
Nhiêu đó hết tài năng rồi, mình mới lớp 3 thôi.

1. "Ví của tôi" hoạt động như thế nào?
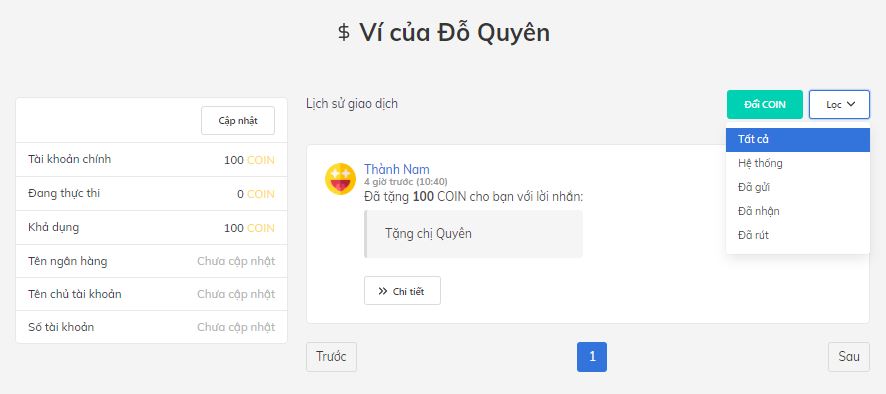
Khi vào ví của mình, các bạn sẽ thấy COIN, 1 COIN = 1000 VNĐ. Các bạn có thể rút COIN bằng cách gửi yêu cầu chuyển tiền về tài khoản ngân hàng, hoặc đổi ra thẻ điện thoại. Chỉ có thể rút COIN khi số COIN trong tài khoản khả dụng từ 50 trở lên.
Lưu ý: Tên ngân hàng, tên chủ tài khoản, số tài khoản và số điện thoại cần cập nhật chính xác để hệ thống có thể chuyển tiền/thẻ điện thoại cho bạn.
Trong lịch sử giao dịch, các bạn có thể kiểm tra trạng thái nhận, gửi, rút COIN của mình.
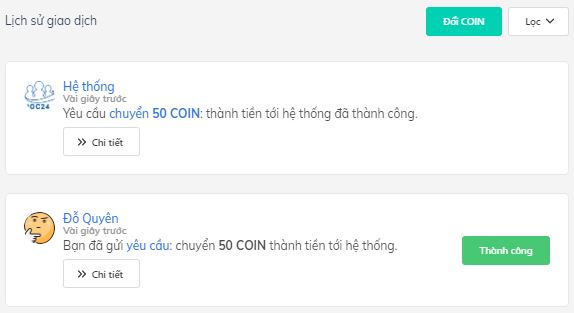
Ngoài ra, các bạn có thể tặng COIN từ ví của mình cho tài khoản của bạn khác nữa nhé.
2. Làm sao để được COIN?
Hiện tại, có năm cách để được COIN trong "ví của tôi".
- Trả lời hỏi đáp nhanh nhất và được giáo viên tick đúng 2GP.
Câu trả lời đúng đưa ra trong vòng 20 phút sau câu hỏi sẽ được cộng 2 COIN.
Câu trả lời đúng đưa ra trong vòng 20-40 phút sau câu hỏi sẽ được cộng 1 COIN.
Giáo viên, CTV chỉ tick một câu trả lời đúng nhất, sớm nhất, trình bày đẹp nhất cho mỗi câu hỏi. Không tick câu trả lời copy.
- Đóng góp nội dung cho Hoc24.
Trong nội dung lí thuyết của các bài học, có chức năng "các phiên bản chỉnh sửa", với những bài học chưa có nội dung (đặc biệt phần Soạn văn, Tập làm văn mẫu), các bạn có thể vào tạo nội dung, giáo viên sẽ duyệt, hiện thị nội dung đó và tặng coin xứng đáng với bài đóng góp.
Nếu bạn nào copy từ các trang khác bị nhắc nhở quá 3 lần sẽ bị khóa chức năng này.
- Được giải thưởng tuần (50 COIN).
- Được thăng hạng GP (từ thiếu tá lên trung tá: 10 COIN, trung tá lên thượng tá: 15 COIN, thượng tá lên đại tá: 20 COIN,...).
- Được người khác tặng.
Ngoài ra, các bạn có thể được thưởng COIN từ các cuộc thi; CTV, thành viên tích cực cuối mỗi kì.
3. COIN để làm gì?
Trước hết, COIN làm giàu "ví của tôi" để đổi ra tiền mặt/thẻ điện thoại. Đó là một phần thưởng và là sự ghi nhận của Hoc24 cho những đóng góp, cố gắng của các bạn.
COIN còn để tặng cho những bạn bè Hoc24 ở xa của mình kèm theo những lời nhắn nhủ, động viên.
Sau này, COIN còn có thể được dùng để mua các ấn phẩm, quà tặng của Hoc24 và nâng cấp tài khoản Hoc24 VIP.
Chúng ta hãy cùng trải nghiệm chức năng mới này và hoạt động tích cực để nhận được COIN một cách xứng đáng nhé!

Kham khảo đề tự luận này nè bọn mình thi chúng đấy
Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức:
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Tham khảo nek :
Bài 1: (3 điểm) Giải phương trình và bất phương trình:
C) x – 2)2 + 2(x – 1) ≤ x2 + 4
Bài 2: (2 điểm) Một ô tô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường AB.
Bài 3: (1 điểm)Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
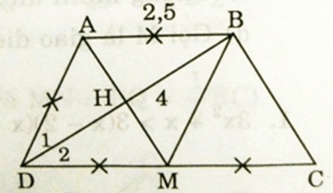
Bài 4: (4 điểm) Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Đáp án và Hướng dẫn giải
Bài 1
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Bài 2
Gọi x (km) là quãng đường AB (x > 0)
Thời gian đi từ A đến B là: x/60 (giờ)
Thời gian đi từ B về A là: x/45 (giờ)
Theo đề ra, ta có phương trình:
⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)
Trả lời: Quãng đường AB dài 180km.
Bài 3
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Bài 4
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
Xét tam giác vuông AHB, ta có :
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
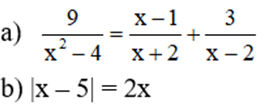
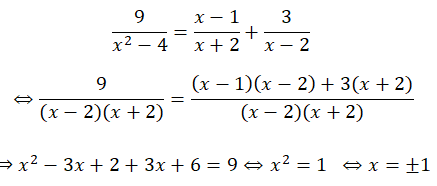
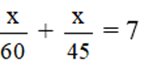
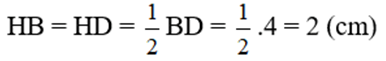
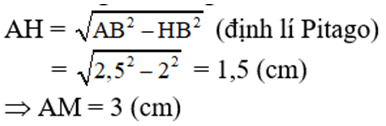
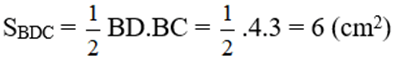
kiếm
kiểu j vậy:))