Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đó là định lý vì tiên đề là qua 1 điểm ở ngoài dg thg ......
c/m: kẻ xy và zt và ff căt xy = A ;cắt zt =B ; theo gt có 1 cặp góc so le = nhau
lấy 1 diem C bất kỳ dựng 1 góc = góc so le tai A ......
Từ đó ta c/m ABCD là hình bình hành => xy // zt
( mk làm z đó, các bn cho ý kiến)

a) Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.

Hỏi nhiều quá , mà thà bạn nói ko cần vẽ hình thì còn giải , đằng này đã vẽ hình còn phải ghi GT , KL . mệt !!!!!!!!!!! @_@
Chứng Minh Định lý hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau

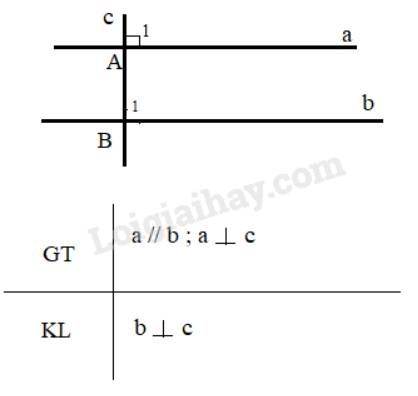
Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b. Thật vậy:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)
Vậy một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Trong chứng minh trên, ta đã sử dụng tính chất của hai đường thẳng song song.

d:
Giả thiết: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
Kết luận: \(\widehat{xAy}=\widehat{x'Ay'}\)

Bài 1:
| GT | a\(\perp\)b;b\(\perp\)c |
| KL | a//c |
Ta có: a\(\perp\)b
b\(\perp\)c
Do đó: a//c(Định lí 1 từ vuông góc tới song song)
Bài 2:
| GT | a\(\perp\)b;b//c |
| KL | a\(\perp\)c |
Ta có: b//c
a\(\perp\)b
Do đó: a\(\perp\)c
Áp dụng được luôn nha bạn, tại nếu đã là định lí được ghi rõ trong SGK thì được áp dụng thoải mái
Cái này là sử dụng luôn em ơi, còn việc chứng minh là nằm trên lí thuyết của bài giảng rồi em.