Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
Tương tự các bài trên.
- Gọi t là thời gian từ lúc rơi cho tới khi chạm đất.
Ta có: h = s = (quãng đường vật rơi) (1)
- Gọi h' là quãng đường vật rơi đến trước khi chạm đất 1 giây:
h' = s' = (t – 1)2. (2)
Gọi ∆h là quãng đường vật rơi (đi được) trong giây cuối cùng:
∆h = h - h' = 15m (3)
Thay (1), (2) vào (3):
=> -
(t2 – 2t + 1) = 15
=> gt - = 15 => t =
= 2s
Thay t = 2s vào (1) => h = = 20m.

Áp dụng công thức đường đi của sự rơi tự do
s = \(\Rightarrow\) t =
với s = h = 20m; g = 10 m/s2.
\(\Rightarrow\) t = √22 s \(\Rightarrow\) t = 2s
Chọn B.
Áp dụng công thức đường đi của sự rơi tự do
s = => t =
với s = h = 20m; g = 10 m/s2.
=> t = √22 s => t = 2s
Chọn B.

a) Chọn gốc thế năng tại mặt đất.
Cơ năng của vật tại vị trí ném: \(W_1=mgh_1+\dfrac{1}{2}mv_1^2\)
Cơ năng vật ở độ cao cực đại: \(W_2=mgh_2\)
Mà ta có: \(W_1=W_2\)
\(\Rightarrow mgh_1+\dfrac{1}{2}mv^2_1=mgh_2\) \(\Rightarrow gh_1+\dfrac{1}{2}v_1^2=gh_2\)
Với \(\left\{{}\begin{matrix}g=10\\h_1=40m\\v_1=10\end{matrix}\right.\) \(\Rightarrow h_2=45m\)
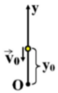
b) Ta vẫn chọn gốc thế năng tại vị trí cũ. 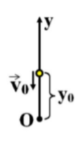
\(y=y_0+v_0t-\dfrac{1}{2}gt^2=40-10t-\dfrac{1}{2}\cdot10\cdot t^2=0\)
( vì khi vật chạm đất thì y=0) \(\Rightarrow t=2s\)
c) Thời gian vật rơi khi chạm đất: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot40}{10}}=2\sqrt{2}s\)
Vận tốc vật khi chạm đất:
\(v=\sqrt{v^2_0+\left(gt\right)^2}=\sqrt{10^2+\left(10\cdot2\sqrt{2}\right)^2}=30\)m/s
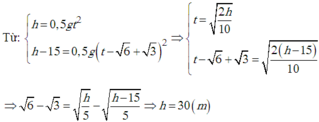
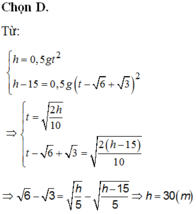

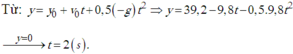
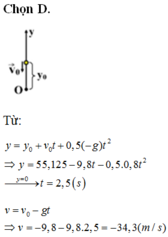
Gọi độ cao ban đầu của viên sỏi là h (m) thời gian rơi hết độ cao h là t.
Ta có:
Quãng đường vật rơi được trước khi chạm đất 1 giây (tức là rơi được t’ = t -1 s) là:
Theo đề ta có: h – h’ = 15 (3)
Thế (1), (2) vào (3)