Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}3x+1\ge2x+7\\4x+3>2x+19\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge6\\2x>16\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ge6\\x>8\end{matrix}\right.\) \(\Rightarrow x>8\)
Ko có đáp án nào giống hoàn toàn, đáp án C là tập con của \(\left(8;+\infty\right)\) nên chấp nhận cũng được

1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)




a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y < }.
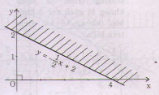
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0) (d).
Ta thấy: 0 < - 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)

1 ) \(|\) x+2 \(|\) - \(|\) x-1 \(|\) < x - 3/2
TH1 : x < -2
bpt <=> -x - 2 - ( -x + 1) < x - 3/2
<=> x > -3/2 ( k tm )
TH 2 : -2 \(\le\) x < 1
bpt <=> x + 2 - ( -x+1) < x - 3/2
<=> x < -5/2 (k tm )
TH3 : x \(\ge\) 1
bpt <=> x + 2 - ( x - 1 ) < x - 3/2
<=> x > 9/2 tm
Vậy x > 9/2 .
2 ) x(x - 1)2 \(\ge\) 4 - x
<=> x( x2 - 2x +1 + 1 ) \(\ge\) 4
<=> x3 - 2x2 + 2x - 4 \(\ge\) 0
<=> x2 (x - 2) + 2(x - 2) \(\ge\) 0
<=> (x2 + 2)(x - 2) \(\ge\) 0
Có : x2 + 2 > 0 , với mọi x
=> x - 2 \(\ge\) 0 <=> x \(\ge\) 2 .
Xem thử đúng hay sai ...
Hoàng Thị Ánh Phương , Ribi Nkok Ngok, Nguyễn Lê Phước Thịnh, Trần Quốc Khanh, Vũ Minh Tuấn, ?Amanda?, Nguyễn Ngọc Lộc , Trên con đường thành công không có dấu chân của kẻ lười biếng, Bùi Lan Anh , Akai Haruma, @Nguyễn Việt Lâm, ...