Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\left\{{}\begin{matrix}x>2\\\frac{5}{2}+3\le x+\frac{3}{2}x\\2x\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>2\\\frac{5}{2}x\ge\frac{11}{2}\\x\le\frac{5}{2}\end{matrix}\right.\) \(\Rightarrow\frac{11}{5}\le x\le\frac{5}{2}\)
\(\Rightarrow a+b=\frac{11}{5}+\frac{5}{2}=D\)
2.
\(\left\{{}\begin{matrix}6x-4x>7-\frac{5}{7}\\4x-2x< 25-\frac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>\frac{22}{7}\\x< \frac{47}{4}\end{matrix}\right.\)
\(\Rightarrow\frac{22}{7}< x< \frac{47}{4}\Rightarrow x=\left\{4;5...;11\right\}\) có 8 giá trị
3.
\(\left\{{}\begin{matrix}5x-4x< 5+2\\x^2< x^2+4x+4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< 7\\x>-1\end{matrix}\right.\)
\(\Rightarrow-1< x< 7\Rightarrow x=\left\{0;1;...;6\right\}\)
\(\Rightarrow\sum x=1+2+...+6=21\)
4.
\(\left\{{}\begin{matrix}x^2-2x+1\le8-4x+x^2\\x^3+6x^2+12x+8< x^3+6x^2+13x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\le7\\x\ge-1\end{matrix}\right.\) \(\Rightarrow-1\le x\le\frac{7}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{min}=-1\\x_{max}=3\end{matrix}\right.\) \(\Rightarrow S=2\)
5.
\(\left\{{}\begin{matrix}x>\frac{1}{2}\\x< m+2\end{matrix}\right.\)
Hệ đã cho có nghiệm khi và chỉ khi:
\(m+2>\frac{1}{2}\Rightarrow m>-\frac{3}{2}\)

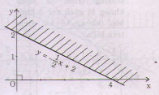
a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y < }.
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0) (d).
Ta thấy: 0 < - 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)