Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Khi quay tam giác BMC quanh cạnh AB tạo ra 2 khối tròn xoay có thể tích là
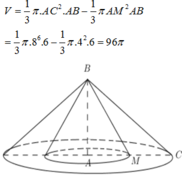

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
B A C M
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1/2 BC
Vì G là trọng tâm của ∆ ABC nên AG = 2/3 AM AM => AG = 2/3.1/2 BC
=> AG = 1/3 BC = 1/3.5 = 1.7cm

Đáp án D
Xét khối nón tròn xoay ( N 1 ) được tạo thành khi quay tam giác AMN quanh trục A B ⇒ N 1 có bán kính đáy r 1 = M N = 2 ; chiều cao h 1 = A M = 5 . Suy ra thể tích khối nón ( N 1 ) là V 1 = 1 3 πr 1 2 h = 1 3 π . 2 2 . 5 = 20 π 3 .
Xét khối nón tròn xoay N 2 được tạo thành khi quay tam giác ABC
quanh trục A B ⇒ N 2 có bán kính đáy r 2 = B C = 4 ; chiều cao h 2 = A B = 10 .
Suy ra thể tích khối nón N 2 là V 2 = 1 3 πr 2 2 h 2 = 1 3 π . 4 2 . 10 = 160 π 3 .
Vậy thể tích khối tròn xoay cần tính là V = V 1 - V 2 = 160 π 3 - 20 π 3 = 140 π 3 .

Đáp án C
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ΔABC, gọi H là chân đường cao của A đến BC. Ta có

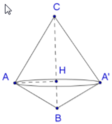

Đáp án C
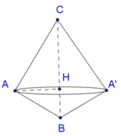
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ∆ A B C , gọi là H chân đường cao của A đến BC. Ta có


a: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao
b: Ta có: ΔABC cân tại A
mà AI là đường cao
nên I là trung điểm của BC
Xét ΔABC có
AI là đường trung tuyến
BD là đường trung tuyến
AI cắt BD tại M
Do đó: M là trọng tâm của ΔABC
c: BM=CM=BC/2=3(cm)
Xét ΔABM vuông tại M có
\(AB^2=AM^2+MB^2\)
hay AM=4(cm)

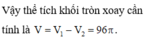

Đáp án D