K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2
2

NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
Do \(\widehat{AOB}\) là góc ở tâm chắn cung AB và \(\widehat{ACB}\) là góc nội tiếp chắn cung AB
\(\Rightarrow\widehat{AOB}=2\widehat{ACB}=90^0\)
\(\Rightarrow\Delta OAB\) vuông cân tại O
Áp dụng định lý Pitago:
\(OA^2+OB^2=AB^2\)
\(\Leftrightarrow R^2+R^2=a^2\)
\(\Rightarrow R^2=\dfrac{a^2}{2}\Rightarrow R=\dfrac{a\sqrt{2}}{2}\)

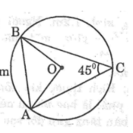
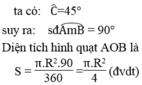
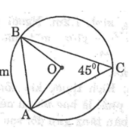

Xét đường tròn(O) có góc ABC là góc nội tiếp chắn cung AB
Mà góc ABC=\(45^o\)\(\Rightarrow\)góc AOB=\(90^o\)\(\Rightarrow\)▲AOB vuông cân tại O
\(AO^2\)+\(OB^2\)=\(AB^2\)
\(2AO^2\)=\(AB^2\)
AO=\(\dfrac{a\sqrt{2}}{2}\)
Vậy bán kính đường tròn là: R=\(\dfrac{a\sqrt{2}}{2}\)
đề yêu cầu tính độ dài cung nhỏ AB mà ạ? Chứ có phải bán kính đường tròn đâu ạ!