Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

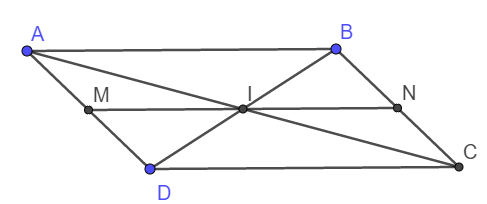
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)

1.Giải:
a. Vì tam giác ABC vuông tại A và AM = \(\frac{1}{2}\)BC
=> AM là đường trung tuyến ứng với cạnh BC
=> M là trung điểm của cạnh BC
=> AM = BM = \(\frac{1}{2}\)BC
Vì AM = BM => Tam giác ABM cân tại M
b. Vì N là trung điểm của AB
=> MN là đường trung tuyến ứng với cạnh AB của tam giác ABM
Mà tam giác ABM cân tại M ( câu a )
=> MN đồng thời là đường cao xuất phát từ M của tam giác ABM
=> \(MN\perp AB\)
Do đó: MN//AC (cùng vuông góc với AB)
=> MNAC là hình thang
Mặt khác: \(\widehat{NAC}\)= \(^{90^0}\)(gt)
=> Tứ giá MNAC là hình thang vuông.

1.áp dụng pi-ta-go ta có : \(AC^2=BC^2-AB^2\Rightarrow AC=\sqrt{100-36}\)\(=8\)
MH là đường trung bình tam giác ABC nên MH=1/2 AB = 3cm
2.Có H là trung điểm MD vì M đối xứng với D qua H
H là trung điểm AC (giả thiết)
tứ giác ANCD có 2 đường chéo giao nhau tại trung điểm mỗi đường nên là hình b hành
3. chưa nghĩ ra
4 tương tự bà trên mk giải rồi bạn tư duy nhé !
3 nè
xét tam giác KHC và tam giác GHA có HC=HA . góc CHK=góc AHG đối đỉnh . góc KCH=góc GAH (so le trong)
nên tam giác KHC = GHA => KC=AG .lại có DC=AM suy ra \(\frac{CK}{CD}=\frac{AG}{AM}\)mà G là trọng tâm tam giác ABC nên AG/AM=2/3
=> CK/CD =2/3 (điều phải cm)

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
a: Xét ΔABC có DE//BC
nên AE/AC=AD/AB
=>AE/10=3/7
hay AE=30/7(cm)
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM(1)
Xét ΔACM có EI//MC
nên EI/MC=AI/AM(2)
Từ (1) và (2) suy ra DI/BM=EI/MC
=>DI=EI
hay I là trung điểm của DE