Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


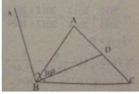
Tia BD nằm giữa hai tia BA và BC nên
∠ABC = ∠ADB + ∠DBC ; ∠DBC =∠ABC - ∠ADB
∠DBC = 55 0 - 30 0 = 25 0
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có∠ABx = ∠DBx - ∠DBA= 90 0 - 30 0 = 60 0
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có ∠ABx = ∠DBx + ∠DBA= 90 0 + 30 0 = 120 0

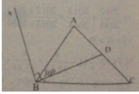
Tia BD nằm giữa hai tia BA và BC nên
A B C ^ = A D B ^ + D B C ^ ; D B C ^ = A B C ^ - A D B ^
D B C ^ = 55 ° - 30 ° = 25 °
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ - D B A ^ = 90 ° - 30 ° = 60 °
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ + D B A ^ = 90 ° + 30 ° = 120 °

Giải
a) Xét \(\Delta ABC\) ta có :
\(\widehat{B}=\widehat{A}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
\(\widehat{B}=90^0+32^0=180^0\)
\(\widehat{B}=122^0=180^0\)
\(\widehat{B}=180^0-122^0=58^0\)
b)
Theo bài ra ta có : \(\widehat{A}:\widehat{B}:\widehat{C}=2:7:1\)
\(\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}\)
Lại có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2+7+1}=\dfrac{180^0}{10}=18^0\)
\(+)\)\(\dfrac{\widehat{A}}{2}=18^0\Rightarrow\widehat{A}=18^0\times2=36^0\)
\(+)\)\(\dfrac{\widehat{B}}{7}=18^0\Rightarrow\widehat{B}=18^0\times7=126^0\)
\(+)\)\(\dfrac{\widehat{C}}{1}=18^0\Rightarrow\widehat{C}=18^0\times1=18^0\)
c)
Xét \(\Delta ABC\) ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí trong 3 góc cùng 1 tam giác )
\(\widehat{A}+75^0+\widehat{C}=180^0\)
\(\widehat{A}+\widehat{C}=180^0-75^0\)
\(\widehat{A}+\widehat{C}=105^0\)
Theo bài ra ta có :
\(\widehat{A}:\widehat{C}=3:2\Rightarrow\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{C}}{2}=\dfrac{\widehat{A}+\widehat{C}}{3+2}=\dfrac{105^0}{5}=21^0\)
\(+)\)\(\dfrac{\widehat{A}}{3}=21^0\Rightarrow\widehat{A}=21^0\times3=63^0\)
\(+)\)\(\dfrac{\widehat{C}}{2}=21^0\Rightarrow\widehat{C}=21^0\times2=42^0\)

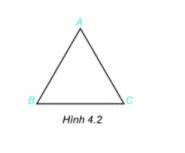
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Gọi số đo các góc A,B,C lần lượt là :a,b,c
Theo đề bài ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a+b+c=180*
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{180^o}{15}=12\)
\(\frac{a}{3}=12\Rightarrow a=12.3=36\)
\(\frac{b}{5}=12\Rightarrow12.5=60\)
\(\frac{c}{7}=12\Rightarrow12.7=84\)
Vậy số đo các góc A,B,C lần lượt là:36 ;60 ;84
áp dụng công thức mà ra