K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PA
0


DG
29 tháng 10 2020
a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.

CM
29 tháng 4 2017
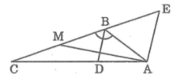

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()
a: Xét ΔBAC có BD là phângíac
nên AD/AB=CD/BC
=>AD/4=CD/1
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được;
\(\dfrac{AD}{4}=\dfrac{CD}{1}=\dfrac{AD+CD}{4+1}=\dfrac{40}{5}=8\)
DO đó: CD=8(cm)
b: Gọi H là trung điểm của BC
=>AH là đừog cao của ΔABC
HB=HC=BC/2=5cm
\(AH=\sqrt{40^2-5^2}=15\sqrt{7}\left(cm\right)\)
\(\cos C=\dfrac{CH}{AC}=\dfrac{5}{40}=\dfrac{1}{8}\)