Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

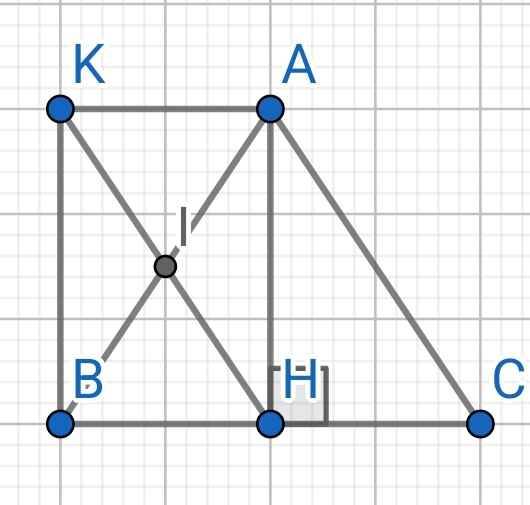 a) Do H và K đối xứng nhau qua I
a) Do H và K đối xứng nhau qua I
⇒ I là trung điểm của HK
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
⇒ ∠AHB = 90⁰
Tứ giác AHBK có:
I là trung điểm HK (cmt)
I là trung điểm AB (gt)
⇒ AHBK là hình bình hành
Mà ∠AHB = 90⁰ (cmt)
⇒ AHBK là hình chữ nhật
b) ∆ABC cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm BC
Mà I là trung điểm AB (gt)
⇒ HI là đường trung bình của ∆ABC
⇒ HI // AC
Tứ giác ACHI có:
HI // AC (cmt)
⇒ ACHI là hình thang
c) ∆ABC đều
⇒ ∠BAC = ∠ACB = 60⁰
⇒ ∠IAC = ∠ACH = 60⁰
Mà ACHI là hình thang (cmt)
⇒ ACHI là hình thang cân

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

a: Xét tứ giác AEBD có
H là trung điểm của AB
H là trung điểm của DE
Do đó: AEBD là hình bình hành
mà \(\widehat{ADB}=90^0\)
nên AEBD là hình chữ nhật
b: Xét tứ giác AHDC có DH//AC
nên AHDC là hình thang

xét tứ giác AMCA có:
IK = IM (gt)
IA =IC (gt)
Suy ra :Tứ giác AMCK là hình bình hành
Mặt khác thì góc M =90
Suy ra :tứ giác AMCH là hình chữ nhật (đpcm)
b) TA có; IM là đường trung bình của tam giác ABC
Suy ra; MI // AB ,MI= 1/2 AB
suy ra; M K= AB, MK // AB
Vậy AKMB là hình bình hành
c) em k bt

c. Hình chữ nhật ADBH là hình vuông \(\Leftrightarrow\) AB vuông góc HD
Mà AC // HD (do ADHC là hình bình hành)
\(\Leftrightarrow\) AB vuông góc với AC
\(\Leftrightarrow\) góc BAC = 90 độ
\(\Leftrightarrow\) tam giác ABC vuông tại A
Vậy, khi tam giác ABC vuông cân tại A thì tứ giác ADBH là hình vuông .
a. Vì EH =HD , AH =BH
=> Tứ giác AEBD là hình bình hành ( tính chất)
a) E là điểm đối xứng của D qua H
\(\Rightarrow\) HE = HD
Tứ giác AEBD có HE = HD; HA = HB
\(\Rightarrow\)AEBD là hình bình hành
mà có \(\widehat{ADB}\)= 900
\(\Rightarrow\)hình bình hành AEBD là hình chữ nhật
b) \(\Delta ABC\)cân tại A, có AD là đường cao
\(\Rightarrow\)AD là đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DB = DC
\(\Delta ABC\)có HA = HB; DB = DC
\(\Rightarrow\)HD là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)HD // AC
\(\Rightarrow\)Tứ giác AHDC là hình thang