Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là trung điểm BC suy ra BH = CH = 30cm
Do tam giác ABC cân tại A nên dễ dàng chứng minh được tam giác BEC = tam giác CDB (cgc)
=> BE = CD
mà AB = AC
nên AE = AD tức là tam giác AED cân tại A
Lại có: áp dụng định lý Pitago vào tam giác vuông AHC
ta tính được AH = 40cm
do đó diện tích tam giác ABC = S(ABC) = 1/2 . AH. BC = 1200
mà S(ABC) = 1/2 . BD. AC suy ra BD = 48cm
Áp dụng Pitago vào tam giác vuông ABD
tính được AD = 14cm
Mặt khác, do AD = AE và AB = AC
nên DE // BC
áp dụng định lý Ta-lét ta được: AD/AC = DE/BC
suy ra DE = 288/5

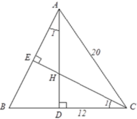
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm.
Đáp án: C

áp dụng tính chất đường phân giác ta có : AD/DC=AB/BC hay AD/AB=DC/BC
theo tính chất của dãy tỉ số bằng nhau, ta co: AD/AB=DC/BC =( AD+DC)/ (AB+BC)=6/10=3/5
VẬY AD = 3/5 x AB=3/5 x 6 =18/5 cm
Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là:

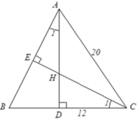
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm => AH = AD - HD = 16 - 9 = 7cm
Đáp án: B

a: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
góc B chung
=>ΔABD đồng dạng với ΔCBE
b:
ΔABC cân tại A có AD là đường cao
nên D là trung điểm của BC
=>DB=DC=12/2=6cm
=>AD=8cm
ΔABD đồng dạng với ΔCBE
=>BE/BD=AB/CB=AD/CE
=>BE/6=10/12=8/CE
=>BE=5cm; CE=12*8/10=9,6cm
c: Xét ΔCDH vuông tại D và ΔCEB vuông tại E có
góc HCD chung
=>ΔCDH đồng dạng với ΔCEB
=>HD/EB=CD/CE
=>HD/5=6/9,6=5/8
=>HD=25/8cm

b: Xét ΔADB và ΔAEC có
\(\widehat{A}\) chung
\(\widehat{ABD}=\widehat{ACE}\left(=\dfrac{1}{2}\widehat{ABC}\right)\)
Do đó: ΔADB\(\sim\)ΔAEC

a) \(\Delta ABC\) cân nên đường cao AD cũng là trung tuyến => BD = DC = 30 cm
Áp dụng Pitago trong tam giác vuông ADB ta tính được AD = 40 cm
Ta giác vuông ABD ~ CHD (g.g)
=> \(\frac{AB}{CH}=\frac{AD}{CD}\) hay CH = \(\frac{AB.CD}{AD}=\frac{150}{4}\) cm
Xét \(\Delta ABD\) và \(\Delta CHD\) có :
\(\widehat{ADB}=\widehat{HDC}=90^o;\widehat{BAD}=\widehat{HCD}\) (cùng phụ với \(\widehat{ABD}\))
\(\Rightarrow\) \(\Delta ABD\) = \(\Delta CHD\)