Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
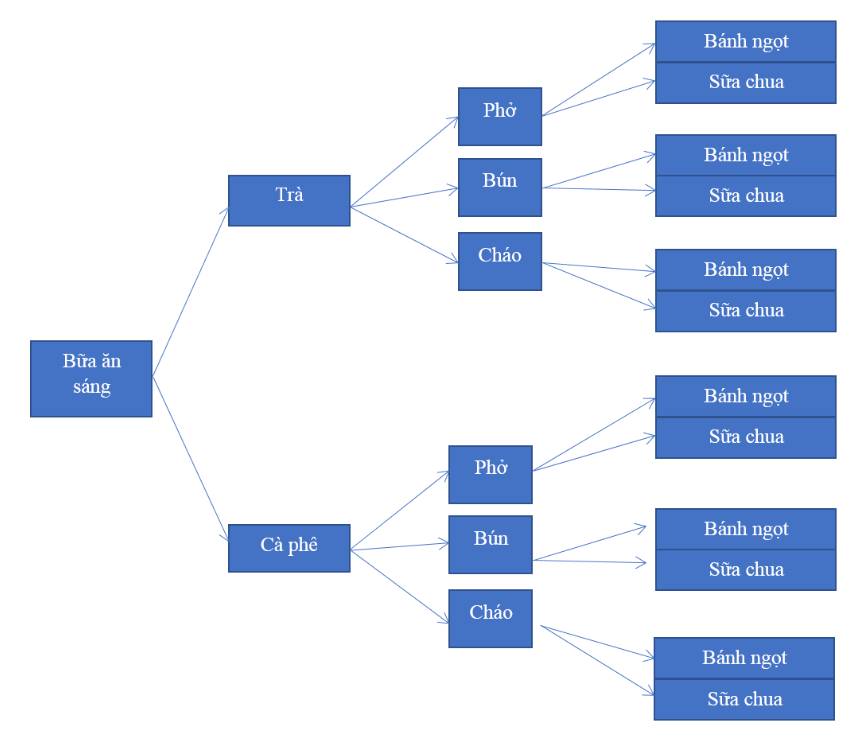
b) Dựa vào sơ đồ cây, ta có số cách chọn khẩu phẩn ăn gồm: 1 đổ uống, 1 món ăn và l món tráng miệng là: 12 (cách chọn)

Để chọn một loại đồ uống là thực hiện một trong ba hành động sau:
Chọn một loại trà sữa: có 5 cách chọn.
Chọn một loại nước hoa quả: có 6 cách chọn
Chọn một loại sinh tố: có 4 cách chọn.
Vậy có 5 + 6+4 =15 cách chọn một loại đồ uống.
Việc chọn một loại đồ uống là thực hiện một trong ba hành động sau:
Chọn một loại trà sữa: có 5 cách chọn.
Chọn một loại nước hoa quả: có 6 cách chọn.
Chọn một loại sinh tố: có 4 cách chọn.
Vậy có 5 + 6 + 4 = 15 cách chọn một loại đồ uống.

15 triệu đồng = 15000 nghìn đồng
Từ giả thiết bài toán ta có bất phương trình \(p\left( x \right) \ge 15000 \Leftrightarrow - 30{x^2} + 2100x - 15000 \ge 15000\)
\( \Rightarrow - 30{x^2} + 2100x - 30000 \ge 0\)
Xét tam thức \(f\left( x \right) = - 30{x^2} + 2100x - 30000\) có \(\Delta = 810000 > 0\), có hai nghiệm phân biệt là \({x_1} = 20,{x_2} = 50\) và \(a = - 30 < 0\)
Ta có bảng xét dấu như sau

Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng 20 đến 50 nghìn đồng.

+) Chọn một cái kem que: Có 5 cách (có thể chọn 1 trong 5 cái)
+) Chọn một cái kem ốc quế: Có 4 cách (có thể chọn 1 trong 4 cái)
Vậy tổng cả 9 cách chọn một trong 9 cái kem cả hai loại trong cửa hàng này.

a) Gọi x, y lần lượt là số lượng cốc cho đồ uống thứ nhất và thứ hai cần tìm.
Lượng calo trong cả 2 đồ uống là: 60x+60y
Lượng vitamin A trong 2 đồ uống là: 12x+6y
Lượng vitamin C trong 2 đồ uống là: 10x+30y
Ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}60x + 60y \ge 300\\12x + 6y \ge 36\\10x + 30y \ge 90\end{array} \right.\)
b)
+) Ta có:
60.2+60.4=360>300
2.12+4.6=48>36
2.10+4.30=140>90
=> (2;4) là một nghiệm của hệ.
+) Ta có:
1.60+5.60=360>300
1.12+5.6=42>36
1.10+5.30=160>90
=> (1;5) là một nghiệm của hệ.
Vậy hai phương án bác Ngọc có thể chọn là:
Phương án 1: 2 cốc loại 1 và 4 cốc loại 2.
Phương án 2: 1 cốc loại 1 và 5 cốc loại 2.

a) Số kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm là: \(C_{20}^3\) ( kết quả )
b) Chọn ngẫu nhiên 3 sản phẩm từ 20 sản phẩm ta được một tổ hợp chập 3 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^3\)( phần tử)
Gọi A là biến cố “Cả 3 sản phẩm được chọn là chính phẩm”
Để chọn được cả 3 sản phẩm đều là chính phẩm thì ta phải chọn 3 sản phẩm từ 16 chính phẩm tức là ta được một tổ hợp chập 3 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^3\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^3}}{{C_{20}^3}} = \frac{{28}}{{57}}\).

Gọi x là số phòng 3 người, y là số phòng 2 người, z là số phòng 1 người, ta được hệ phương trình
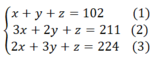
Cách 1. Dùng máy tính cầm tay.
Cách 2. Khử z để đưa về hệ phương trình hai ẩn. Trừ vế theo vế phương trình (2) cho phương trình (1) và phương trình (2) cho phương trình (3) ta được hệ phương trình
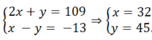
Từ đó thay vào (1) ta được z = 25.
Vậy đáp án là B.
Cách 3. Tính nhẩm.
Với phương án A, vế trái của phương trình (2) bằng 243 nên bị loại. Với phương án C, vế trái của phương trình (3) bằng 245 nên bị loại. Tương tự với phương án D, vế trái của phương trình (3) bằng 245 nên loại.
Đáp án: B

Việc thực hiện bữa trưa gồm một món chính, một món phụ và một loại đồ uống gồm 3 công đoạn
Công đoạn 1: Chọn 1 món chính trong 5 món, có 5 cách chọn
Công đoạn 2: Chọn 1 món phụ trong 3 món, có 3 cách chọn
Công đoạn 3: Chọn 1 loại đồ uống trong 4 loại, có 4 cách chọn
Áp dụng quy tắc nhân, ta có số cách chọn một bữa trưa đầy đủ là
\(5.3.4 = 60\)
Vậy có 60 cách chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống.