Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\left|-1,3\right|-\left|-3,7\right|+\left|-\dfrac{1}{2}\right|\)
\(=1,3-3,7+\dfrac{1}{2}\)
\(=-2,4+\dfrac{1}{2}\)
\(=-2,9\)
b/ \(\left|\dfrac{2}{5}\right|-\left|-0,2\right|.\left|-7\right|\)
\(=\dfrac{2}{5}-0,2.7\)
\(=\dfrac{2}{5}.1,4\)
\(=0,56\)
c/ \(-15:\left|-3\right|+\left|0,5\right|\)
\(=-15:2+0,5\)
\(=-7,5+0,5\)
\(=-8\)

a,\(\left(-\dfrac{5}{6}\right)^6.\left(\dfrac{6}{5}\right)^8=\left[\left(-\dfrac{5}{6}\right)^6.\left(\dfrac{6}{5}\right)^6\right].\left(\dfrac{6}{5}\right)^2=\dfrac{36}{25}\)
b,\(\left(-\dfrac{13}{8}\right)^3.\left(-\dfrac{23}{13}\right)^4=\left[\left(-\dfrac{13}{8}\right)^3.\left(-\dfrac{23}{13}\right)^3\right].\left(-\dfrac{23}{13}\right)=\left(\dfrac{23}{8}\right)^3.\left(-\dfrac{23}{13}\right)\)
c,\(\left(0,2\right)^7.5^{10}=\left(0,2.5\right)^7.5^3=125\)
d,\(\left(-0,1\right)^7.\left(-10\right)^{13}=\left(-0,1.\left(-10\right)\right)^7.\left(-10\right)^6=1000000\)

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)

a/ \(\left|3x-1\right|=\left|5-2x\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5-2x\\3x-1=-5+2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2x=5+1\\3x-2x=-5+1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}5x=6\\x=-4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\\x=-4\end{matrix}\right.\)
Vậy ......
b/ \(\left|x+2\right|-\left|x+7\right|=0\)
\(\Leftrightarrow\left|x+2\right|=\left|x+7\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=x+7\\x+2=-x-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-x=7-2\\x+x=-7-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}0x=5\left(loại\right)\\2x=-9\end{matrix}\right.\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy ...............
c/ \(\left|2x-1\right|+x=2\)
\(\Leftrightarrow\left|2x-1\right|=2-x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=2-x\\2x-1=-2+x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+x=2+1\\2x-x=-2-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=3\\x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Vậy ..

a/ \(\left|-x\right|=1,5\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1,5\\x=-1,5\end{matrix}\right.\)
Vậy .....
b/ \(\left|x+\dfrac{1}{2}\right|=2\dfrac{1}{2}\)
\(\Leftrightarrow\left|x+\dfrac{1}{2}\right|=\dfrac{5}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{5}{2}\\x+\dfrac{1}{2}=-\dfrac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy ....
c/ \(\left|0,5-x\right|=\left|-0,5\right|\)
\(\left|0,5-x\right|=0,5\)
\(\Leftrightarrow\left[{}\begin{matrix}0,5-x=0,5\\0,5-x=-0,5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy ...

a: \(\dfrac{x+1}{5}+\dfrac{x+1}{6}=\dfrac{x+1}{7}+\dfrac{x+1}{8}\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}-\dfrac{1}{8}\right)=0\)
=>x+1=0
hay x=-1
b: \(\Leftrightarrow\left(\dfrac{x-1}{2009}-1\right)+\left(\dfrac{x-2}{2008}-1\right)=\left(\dfrac{x-3}{2007}-1\right)+\left(\dfrac{x-4}{2006}-1\right)\)
=>x-2010=0
hay x=2010
c: \(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+10}+\dfrac{1}{x+10}-\dfrac{1}{x+17}=\dfrac{x}{\left(x+2\right)\left(x+17\right)}\)
\(\Leftrightarrow\dfrac{x}{\left(x+2\right)\left(x+17\right)}=\dfrac{x+17-x-2}{\left(x+2\right)\left(x+17\right)}\)
=>x=15

Bài 1:
a, \(A=3,7+\left|4,3-x\right|\ge3,7\)
Dấu " = " khi \(\left|4,3-x\right|=0\Rightarrow x=4,3\)
Vậy \(MIN_A=3,7\) khi x = 4,3
b, \(B=\left|3x+\dfrac{41}{5}\right|-14,2\ge-14,2\)
Dấu " = " khi \(\left|3x+\dfrac{41}{5}\right|=0\Rightarrow x=\dfrac{-41}{15}\)
Vậy \(MIN_B=-14,2\) khi \(x=\dfrac{-41}{15}\)
c, \(C=\left|4x-3y\right|+\left|5y+7,5\right|\ge17,5\)
( do \(\left|4x-3y\right|+\left|5y+7,5\right|\ge0\) )
Dấu " = " khi \(\left\{{}\begin{matrix}\left|4x-3y\right|=0\\\left|5y+7,5\right|=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-9}{8}\\y=-1,5\end{matrix}\right.\)
Vậy \(MIN_C=17,5\) khi \(\left\{{}\begin{matrix}x=\dfrac{-9}{8}\\y=-1,5\end{matrix}\right.\)
Bài 2:
a, \(A=5,5-\left|2x-1,5\right|\le5,5\)
Dấu " = " khi \(\left|2x-1,5\right|=0\Rightarrow x=0,75\)
Vậy \(MIN_A=5,5\) khi x = 0,75
b, c tương tự

\(\left[\left(-20,83\right).0,2+\left(-9,17\right).0,2\right]:\left[2,47.0,5-\left(-3.53\right).0,5\right]\)
\(=\left\{0,2.\left[\left(-20,83\right)+\left(-9,17\right)\right]\right\}:\left[2,47.0,5+3,53.0,5\right]\)
\(=\left[0,2.\left(-30\right)\right]:\left[0,5.\left(2,47+3,53\right)\right]\)
\(=\left(-6\right):\left(0,5.6\right)\)
\(=\left(-6\right):3\)
\(=\left(-2\right)\)
[ (-20,83) . 0,2 + (-9,17) . 0,2 ] : [ 2,47 . 0,5 - (-3.53) . 0,5 ]
= [\(\frac{-2083}{500}\) + \(\frac{-917}{500}\) ] [ \(\frac{247}{200}-\frac{-353}{200}\) ]
= -6 : 3 = -2


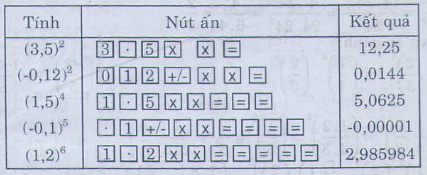
a) (−3,1597)+(−2,39)= -5,5497
b) (−0,793)−(−2,1068)= 1.3138
c) (−0,5).(−3,2)+(−10,1).0,2= -0,42
d) 1,2.(−2,6)+(−1,4):0,7=-5,12