Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
ĐK: \(x\geq 5\)
PT \(\Leftrightarrow \sqrt{4(x-5)}+3\sqrt{\frac{x-5}{9}}-\frac{1}{3}\sqrt{9(x-5)}=6\)
\(\Leftrightarrow \sqrt{4}.\sqrt{x-5}+3\sqrt{\frac{1}{9}}.\sqrt{x-5}-\frac{1}{3}.\sqrt{9}.\sqrt{x-5}=6\)
\(\Leftrightarrow 2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=6\)
\(\Leftrightarrow 2\sqrt{x-5}=6\Rightarrow \sqrt{x-5}=3\Rightarrow x=3^2+5=14\)
2)
ĐK: \(x\geq -1\)
\(\sqrt{x+1}+\sqrt{x+6}=5\)
\(\Leftrightarrow (\sqrt{x+1}-2)+(\sqrt{x+6}-3)=0\)
\(\Leftrightarrow \frac{x+1-2^2}{\sqrt{x+1}+2}+\frac{x+6-3^2}{\sqrt{x+6}+3}=0\)
\(\Leftrightarrow \frac{x-3}{\sqrt{x+1}+2}+\frac{x-3}{\sqrt{x+6}+3}=0\)
\(\Leftrightarrow (x-3)\left(\frac{1}{\sqrt{x+1}+2}+\frac{1}{\sqrt{x+6}+3}\right)=0\)
Vì \(\frac{1}{\sqrt{x+1}+2}+\frac{1}{\sqrt{x+6}+3}>0, \forall x\geq -1\) nên $x-3=0$
\(\Rightarrow x=3\) (thỏa mãn)
Vậy .............

\(a,\sqrt{x-2\sqrt{x}-1}-\sqrt{x-1}=1.\)
\(\Rightarrow\sqrt{\left(\sqrt{x}-1\right)^2}-\sqrt{x-1}=1\)
\(\Rightarrow x-1-\sqrt{x-1}=1\)
\(\Rightarrow\sqrt{x-1}=x-1+1\)
\(\Rightarrow x-1=x^2\Rightarrow x^2-x+1=0\) ( vô nghiệm vì nó luôn lớn hơn 0 )
\(đkxđ\Leftrightarrow2x-1\ge0\Rightarrow x\ge\frac{1}{2}\)
\(c,\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=\sqrt{2}.\)
\(\Rightarrow\sqrt{2x+2\sqrt{2x-1}}+\sqrt{2x-2\sqrt{2x-1}}=2\)
\(\Rightarrow\sqrt{2x-1+2\sqrt{2x-1}+1}+\sqrt{2x-1-2\sqrt{2x-1}+1}=2\)
\(\Rightarrow\sqrt{\left(\sqrt{2x-1}+1\right)^2}+\sqrt{\left(\sqrt{2x-1}-1\right)^2}=2\)
\(\Rightarrow\sqrt{2x-1}+1+\sqrt{2x-1}-1=2\)
\(\Rightarrow\sqrt{2x-1}+\sqrt{2x-1}=2\)
\(\Rightarrow\sqrt{2x-1}=1\Rightarrow\sqrt{2x-1}^2=1\)
\(\Rightarrow2x-1=1\Rightarrow2x=2\Leftrightarrow x=1\)\(\left(tm\right)\)
d tương tự nha , nhân thêm 2 vế với \(\sqrt{6}\)là ra

1) \(\sqrt{\text{x^2− 20x + 100 }}=10\)
<=> \(\sqrt{\left(x-10\right)^2}=10\)
<=> \(\left|x-10\right|=10\)
=> \(\left[{}\begin{matrix}x-10=10\\x-10=-10\end{matrix}\right.\)=> \(\left[{}\begin{matrix}x=10+10\\x=\left(-10\right)+10\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=20\\x=0\end{matrix}\right.\)
Vậy S = \(\left\{20;0\right\}\)
2) \(\sqrt{x +2\sqrt{x}+1}=6\)
<=> \(\sqrt{\left(\sqrt{x^2}+2.\sqrt{x}.1+1^2\right)}=6\)
<=> \(\sqrt{\left(\sqrt{x}+1\right)^2}=6\)
<=> \(\left|\sqrt{x}+1\right|=6\)
=> \(\left[{}\begin{matrix}\sqrt{x}+1=6\\\sqrt{x}+1=-6\end{matrix}\right.\)=>\(\left[{}\begin{matrix}\sqrt{x}=6-1=5\\\sqrt{x}=\left(-6\right)-1=-7\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=25\\x=-49\left(loai\right)\end{matrix}\right.\)
Vậy S = \(\left\{25\right\}\)
3) \(\sqrt{x^2-6x+9}=\sqrt{4+2\sqrt{3}}\)
<=> \(\sqrt{\left(x-3\right)^2}=\sqrt{\sqrt{3^2}+2.\sqrt{3}.1+1^2}\)
<=> \(\left|x-3\right|=\sqrt{\left(\sqrt{3}+1\right)^2}\)
<=> \(\left|x-3\right|=\sqrt{3}+1\)
=> \(\left[{}\begin{matrix}x-3=\sqrt{3}+1\\x-3=-\left(\sqrt{3}+1\right)\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=\sqrt{3}+4\\x=-\sqrt{3}+2\end{matrix}\right.\)
Vậy S = \(\left\{\sqrt{3}+4;-\sqrt{3}+2\right\}\)
4) \(\sqrt{3x+2\sqrt{3x}+1}=5\)
<=> \(\sqrt{\sqrt{3x}^2+2.\sqrt{3x}.1+1^2}=5\)
<=> \(\sqrt{\left(\sqrt{3x}+1\right)^2}=5\)
<=> \(\left|\sqrt{3x}+1\right|=5\)
=> \(\left[{}\begin{matrix}\sqrt{3x}+1=5\\\sqrt{3x}+1=-5\end{matrix}\right.\)=> \(\left[{}\begin{matrix}\sqrt{3x}=5-1=4\\\sqrt{3x}=\left(-5\right)-1=-6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=16\\3x=-6\left(loai\right)\end{matrix}\right.\)=> x = \(\dfrac{16}{3}\) Vậy S = \(\left\{\dfrac{16}{3}\right\}\)
5) \(\sqrt{x^2+2x\sqrt{3}+3}=\sqrt{4-2\sqrt{3}}\)
<=> \(\sqrt{\left(x-\sqrt{3}\right)^2}=\sqrt{\left(\sqrt{3}-1\right)^2}\)
<=> \(\left|x-\sqrt{3}\right|=\sqrt{3}-1\)
<=> \(\left[{}\begin{matrix}x-\sqrt{3}=\sqrt{3}-1\\x-\sqrt{3}=-\left(\sqrt{3}-1\right)\end{matrix}\right.\)=> \(\left[{}\begin{matrix}x=-1\\x=-2\sqrt{3}+1\end{matrix}\right.\)
Vậy S = \(\left\{-1;-2\sqrt{3}+1\right\}\)
6) \(\sqrt{6x+4\sqrt{6x}+4}=7\)
<=> \(\sqrt{\sqrt{6x}^2+2.\sqrt{6x}.2+2^2}=7\)
<=> \(\sqrt{\left(\sqrt{6}+2\right)^2}=7\)
<=> \(\left|\sqrt{6x}+2\right|=7\)
=> \(\left[{}\begin{matrix}\sqrt{6x}+2=7\\\sqrt{6x}+2=-7\end{matrix}\right.\)=>\(\left[{}\begin{matrix}\sqrt{6x}=7-2=5\\\sqrt{6x}=\left(-7\right)-2=-9\left(loai\right)\end{matrix}\right.\)
=> \(\sqrt{6x}=5=>6x=25=>x=\dfrac{25}{6}\)

a)\(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{3}{2}\sqrt{6}+2\frac{\sqrt{6}}{3}-4\frac{\sqrt{6}}{2}\)
\(=\sqrt{6}\left(\frac{3}{2}+\frac{2}{3}-\frac{4}{2}\right)=\sqrt{6}.\frac{1}{6}\)
b) \(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}=\left(x.\frac{\sqrt{6x}}{x}+\frac{\sqrt{6x}}{3}+\sqrt{6x}\right):\sqrt{6x}\)
\(=1+\frac{1}{3}+1=2\frac{1}{3}\)

ĐKXĐ: \(x\ge\frac{1}{2}\).
Phương trình đã cho tương đương với:
\(\sqrt{6x+6+6\sqrt{6x-3}}+\sqrt{6x+6-6\sqrt{6x-3}}=6\)
\(\Leftrightarrow\sqrt{\left(\sqrt{6x-3}+3\right)^2}+\sqrt{\left(\sqrt{6x-3}-3\right)^2}=6\)
\(\Leftrightarrow\sqrt{6x-3}+3+\left|3-\sqrt{6x-3}\right|=6\). (*)
\(\Leftrightarrow3-\sqrt{6x-3}\ge0\Leftrightarrow\sqrt{6x-3}\le3\Leftrightarrow x\le1\).
Vậy nghiệm của pt là: \(\frac{1}{2}\le x\le1\).

1.
ĐKXĐ: $x\geq 1$
PT \(\Leftrightarrow \sqrt{(x-1)-4\sqrt{x-1}+4}+\sqrt{(x-1)+6\sqrt{x-1}+9}=5\)
\(\Leftrightarrow \sqrt{(\sqrt{x-1}-2)^2}+\sqrt{(\sqrt{x-1}+3)^2}=5\)
\(\Leftrightarrow |\sqrt{x-1}-2|+|\sqrt{x-1}+3|=5\)
Ta thấy:
\(\text{VT}=|2-\sqrt{x-1}|+|\sqrt{x-1}+3|\geq |2-\sqrt{x-1}+\sqrt{x-1}+3|=5\)
Dấu "=" xảy ra khi \((2-\sqrt{x-1})(\sqrt{x-1}+3)\geq 0\)
$\Leftrightarrow 2\geq \sqrt{x-1}$
$\Leftrightarrow 5\geq x\geq 1$
2.
ĐKXĐ: $x\geq \frac{5}{2}$
PT \(\Leftrightarrow \sqrt{2x+4-6\sqrt{2x-5}}+\sqrt{2x-4+2\sqrt{2x-5}}=4\)
\(\Leftrightarrow \sqrt{(2x-5)-6\sqrt{2x-5}+9}+\sqrt{(2x-5)+2\sqrt{2x-5}+1}=4\)
\(\Leftrightarrow \sqrt{(\sqrt{2x-5}-3)^2}+\sqrt{(\sqrt{2x-5}+1)^2}=4\)
\(\Leftrightarrow |\sqrt{2x-5}-3|+|\sqrt{2x-5}+1|=4\)
Thấy rằng:
\(\text{VT}=|3-\sqrt{2x-5}|+|\sqrt{2x-5}+1|\geq |3-\sqrt{2x-5}+\sqrt{2x-5}+1|=4\)
Dấu "=" xảy ra khi $(3-\sqrt{2x-5})(\sqrt{2x-5}+1)\geq 0$
$\Leftrightarrow 3-\sqrt{2x-5}\geq 0$
$\Leftrightarrow 7\geq x\geq \frac{5}{2}$
Vậy........

b/ ĐKXĐ: \(x\ge\frac{1}{2}\)
\(\sqrt{2x+2\sqrt{2x-1}}+\sqrt{2x-2\sqrt{2x-1}}=2\)
\(\Leftrightarrow\sqrt{2x-1+2\sqrt{2x-1}+1}+\sqrt{2x-1-2\sqrt{2x-1}+1}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2x-1}+1\right)^2}+\sqrt{\left(\sqrt{2x-1}-1\right)^2}=2\)
\(\Leftrightarrow\left|\sqrt{2x-1}+1\right|+\left|1-\sqrt{2x-1}\right|=2\)
Ta có:
\(\left|\sqrt{2x+1}+1\right|+\left|1-\sqrt{2x-1}\right|\ge\left|\sqrt{2x+1}+1+1-\sqrt{2x-1}\right|=2\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(\sqrt{2x+1}+1\right)\left(1-\sqrt{2x-1}\right)\ge0\)
\(\Leftrightarrow\sqrt{2x-1}\le1\)
\(\Leftrightarrow x\le1\)
Vậy nghiệm của pt là \(\frac{1}{2}\le x\le1\)
c/ ĐKXĐ: \(x\ge\frac{3}{2}\)
\(\sqrt{6x+6\sqrt{6x-9}}+\sqrt{6x-6\sqrt{6x-9}}=6\)
\(\Leftrightarrow\sqrt{\left(\sqrt{6x-9}+3\right)^2}+\sqrt{\left(\sqrt{6x-9}-3\right)^2}=6\)
\(\Leftrightarrow\left|\sqrt{6x-9}+3\right|+\left|3-\sqrt{6x-9}\right|=6\)
Ta có:
\(\left|\sqrt{6x-9}+3\right|+\left|3-\sqrt{6x-9}\right|\ge\left|\sqrt{6x-9}+3+3-\sqrt{6x-9}\right|=6\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(\sqrt{6x-9}+3\right)\left(3-\sqrt{6x-9}\right)\ge0\)
\(\Leftrightarrow\sqrt{6x-9}\le3\Rightarrow x\le3\)
Vậy nghiệm của pt là \(\frac{3}{2}\le x\le3\)

Em xin phép làm bài EZ nhất :)
4,ĐK :\(\forall x\in R\)
Đặt \(x^2+x+2=t\) (\(t\ge\dfrac{7}{4}\))
\(PT\Leftrightarrow\sqrt{t+5}+\sqrt{t}=\sqrt{3t+13}\)
\(\Leftrightarrow2t+5+2\sqrt{t\left(t+5\right)}=3t+13\)
\(\Leftrightarrow t+8=2\sqrt{t^2+5t}\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\ge-8\\\left(t+8\right)^2=4t^2+20t\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\ge\dfrac{7}{4}\\3t^2+4t-64=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\ge\dfrac{7}{4}\\\left(t-4\right)\left(3t+16\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\ge\dfrac{7}{4}\\\left[{}\begin{matrix}t=4\left(tm\right)\\t=-\dfrac{16}{3}\left(l\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow x^2+x+2=4\)\(\Leftrightarrow x^2+x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vậy ....
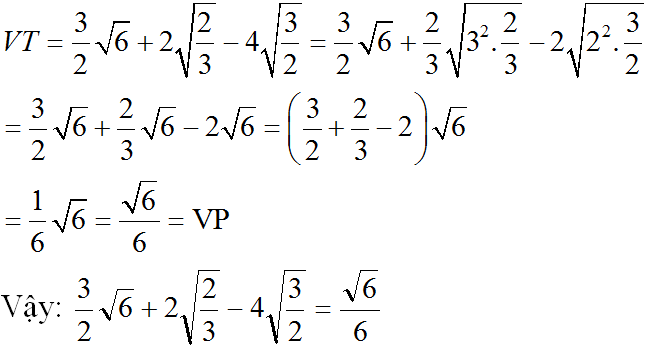
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Bình phương 2 vế:
\(\Leftrightarrow2\left(x+1\right)+2\sqrt{\left(x+1+\sqrt{6x-3}\right)\left(x+1-\sqrt{6x-3}\right)}=6\)
\(\Leftrightarrow x+\sqrt{\left(x+1\right)^2-\left(6x-3\right)}=2\)
\(\Leftrightarrow x+\sqrt{x^2-4x+4}=2\)
\(\Leftrightarrow\sqrt{\left(2-x\right)^2}=2-x\)
\(\Leftrightarrow\left|2-x\right|=2-x\)
\(\Leftrightarrow2-x\ge0\)
\(\Rightarrow x\le2\)
Kết hợp ĐKXĐ ta được nghiệm của pt là: \(\dfrac{1}{2}\le x\le2\)