NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
3 tháng 8 2015
Đẫ bảo là a = -9 thì biểu thức không tính đc mở máy tính ra BẤm thử mà xem
PN
1
DH
24 tháng 6 2017
\(A=\sqrt{9a^2-12a+4}-9a+1\)
\(A=\sqrt{9a^2-6a-6a+4}-9a+1\)
\(A=\sqrt{\left(9a^2-6a\right)-\left(6a-4\right)}-9a+1\)
\(A=\sqrt{3a.\left(3a-2\right)-2.\left(3a-2\right)}-9a+1\)
\(A=\sqrt{\left(3a-2\right)^2}-9a+1\)
\(A=3a-2-9a+1\)
\(A=-6a-1\)
\(A=-\left(6a+1\right)\)
Chúc bạn học tốt!!!
24 tháng 6 2017
gà vc \(\sqrt{\left(3a-2\right)^2}=\left|3a-2\right|\) xét 2 trg hợp
29 tháng 5 2019
\(\frac{\sqrt{9+12a+4a^2}}{\sqrt{b^2}}\)
\(=\frac{\sqrt{\left(2a+3\right)^2}}{\sqrt{b^2}}\)
\(=\frac{2a+3}{-b}\)( theo điều kiện )
HH
29 tháng 9 2020
\(a)\sqrt{-9a}-\sqrt{9+12a+4a^2}\)
\(==\sqrt{3^2.\left(-a\right)}-\sqrt{3^2-2.3.2a+\left(2a\right)^2}\)
\(=3\sqrt{-a}-\sqrt{\left(3+2a\right)^2}\)
\(=3\sqrt{a}-\left|3+2a\right|\)
\(b)1+\frac{3m}{m-2}\sqrt{m^2-4m+4}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m\right)^2-2.2m+2^2}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m-2\right)^2}\)
\(=1+\frac{3m}{m-2}|m-2|\)
\(c)4x-\sqrt{9x^2+6x+1}\)
\(=4x-\sqrt{\left(3x\right)^2+2.3x+1}\)
\(=4x-\sqrt{\left(3x+1\right)^2}\)
\(=4x-|3x+1|\)
15 tháng 7 2017
a) \(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) \(=\sqrt{9.\left(-a\right)}-\sqrt{\left(3+2a\right)^2}=3\sqrt{-a}-\left|3+2a\right|\)
\(=3\sqrt{9}-\left|3+2\left(-9\right)\right|=3.3-15=-6\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4x+4}=1+\dfrac{3m}{m-2}\sqrt{\left(m-2\right)^2}=1+\dfrac{3m\left|m-2\right|}{m-2}\)
\(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m-2\right)>0\right)\\1-3m\left(nến\left(m-2\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m>2\right)\right)\\1-3m\left(nếu\left(m< 2\right)\right)\end{matrix}\right.\)
ta có : \(m=1,5< 2\) vậy giá trị của biểu thức tại m = 1,5 là \(1-3m\) = \(1-3.1,5=-3,5\)
c) \(\sqrt{1-10a+25a^2}-4a=\sqrt{\left(1-5a\right)^2}-4a=\left|1-5a\right|-4a\)
\(=\left\{{}\begin{matrix}1-9a\left(nếu\left(1-5a\right)\ge0\right)\\a-1\left(nếu\left(1-5a\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1-9a\left(nếu\left(a\le\dfrac{1}{5}\right)\right)\\a-1\left(nếu\left(a>\dfrac{1}{5}\right)\right)\end{matrix}\right.\)
ta có : \(a=\sqrt{2}>\dfrac{1}{5}\) vậy giá trị của biểu thức tại \(a=\sqrt{2}\) là a - 1 = \(\sqrt{2}-1\)
d) \(4x-\sqrt{9x^2+6x+1}=4x-\sqrt{\left(3x+1\right)^2}=4x-\left|3x+1\right|\)
\(=\left\{{}\begin{matrix}x-1\left(nếu\left(x\ge-\dfrac{1}{3}\right)\right)\\7x+1\left(nếu\left(x< -\dfrac{1}{3}\right)\right)\end{matrix}\right.\)
ta có : \(x=-\sqrt{3}< -\dfrac{1}{3}\) vậy giá trị của biểu thức tại \(x=-\sqrt{3}\) là \(7.\left(-\sqrt{3}\right)+1=1-7\sqrt{3}\)
AH
Akai Haruma
Giáo viên
30 tháng 6 2019
Lời giải:
\(\sqrt{\frac{9+12a+4a^2}{b^2}}=\sqrt{\frac{(2a)^2+2.2a.3+3^2}{b^2}}=\sqrt{\frac{(2a+3)^2}{b^2}}\)
\(=|\frac{2a+3}{b}|\)
Vì $a>-1,5; b< 0$ nên \(\frac{2a+3}{b}< 0\Rightarrow \sqrt{\frac{9+12a+4a^2}{b^2}}= |\frac{2a+3}{b}|=\frac{-2a-3}{b}\)
\((a-b)\sqrt{\frac{ab}{(a-b)^2}}=(a-b)\sqrt{ab}.\frac{1}{|a-b|}\)
Do $a< b< 0$ nên $a-b< 0\rightarrow |a-b|=b-a$
\(\Rightarrow (a-b)\sqrt{\frac{ab}{(a-b)^2}}=(a-b).\frac{\sqrt{ab}}{|a-b|}=(a-b).\frac{\sqrt{ab}}{b-a}=-\sqrt{ab}\)
T
5 tháng 7 2019
Em thử nha!Sai thì thôi:((
\(A=\left|m+1\right|+\left|m-1\right|=\left|m+1\right|+\left|1-m\right|\ge\left|m+1+1-m\right|=2\)
Dấu"=" xảy ra khi \(\left(m+1\right)\left(1-m\right)\ge0\Leftrightarrow-m^2+1\Leftrightarrow-1\le m\le1\)
\(B=\sqrt{\left(2a\right)^2-2.2a.1+1}+\sqrt{4a^2-2.2a.3+9}\)
\(=\left|2a-1\right|+\left|2a-3\right|=\left|2a-1\right|+\left|3-2a\right|\ge2\)
Dấu "=" xảy ra khi...
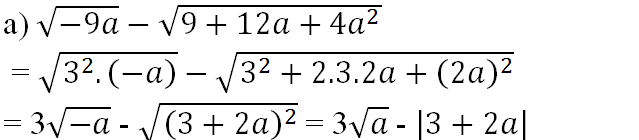
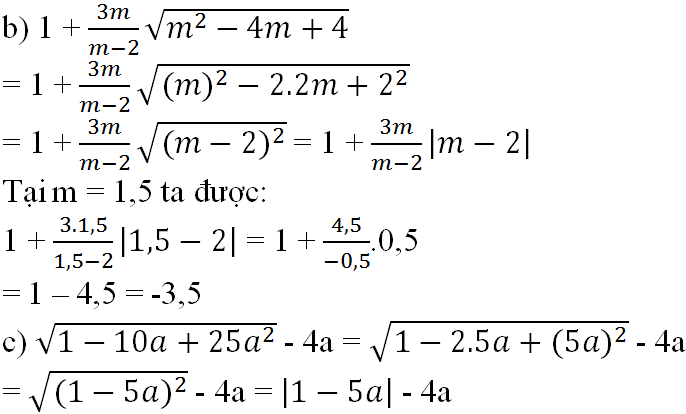
\(\sqrt{-9a}-\sqrt{4a^2+12a+9}=3\sqrt{-a}-\left|2a+3\right|\)
Thay a = -9 vào được kết quả là : -6