Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
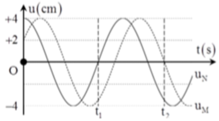
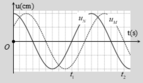
Thời điểm ban đầu t = 0 thì phần tử N ở biên dương, nên pha ban đầu là 0
Ta có phương trình dao động của N là uN = 4.cos (ωt) (cm)
Thời điểm ban đầu phần tử M ở vị trí x0= +2 và chuyển động theo chiều dương=> pha ban đầu là - π 3
Ta có phương trình dao động của M là u M = 4 cos ( ω t - π 3 ) c m
Sóng truyền từ M đến N, ta có thể có: ω . x v = π 3 ⇒ x = v 3 . 2 . f = v T 6 = 10 3 c m
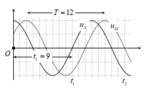
Biên độ của N và M là 4, nên tính từ thời điểm ban đầu đến t1 thì N đi từ biên dướng đến vị trí cân bằng lần 2. Tức là hết ¾.T => T = 4/3.0,05s
Xét phần tử N, từ thời điểm ban đầu đến vị trí t2
Tổng thời gian là: T 6 + T + T 4 = 17 12 T
Vậy t2= 17 12 T
Thay vào phương trình dao động của N tìm được tọa độ của N tại thời điểm t2 là
UN= - 2 3 c m
Khoảng cách của M và N tại thời điểm t2 là :
∆ d = x 2 + ( u M - u N ) 2 = ( 10 3 ) 2 + ( 2 3 ) 2 = 23 c m

Chu kì \(T=2\pi/\omega=2s\)
Bước sóng: \(\lambda=v.T=20.2=40cm\)
M cùng pha với O suy ra \(OM=k\lambda=40k(cm)\)
NM gần nhau nhất dao động vuông pha suy ra \(MN=\dfrac{\lambda}{4}=10cm\)
Căn cứ theo các đáp án ta có thể chọn C là đáp án đúng.

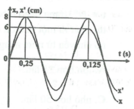
Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.



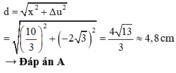
Đáp án A
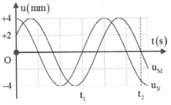
+ Phương trình dao động của hai phần tử M, N là:
Ta thấy rằng khoảng thời gian
+ Độ lệch pha giữa hai sóng:
Thời điểm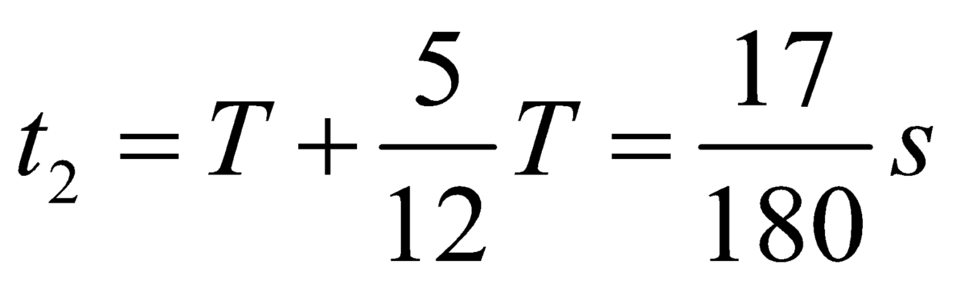
Khi đó điểm M đang có li độ bằng 0 và li độ của điểm N là