PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
3
17 tháng 1 2016
#2 22-02-2014 | ||||
| ||||
n2+404=a2 a2-n2=404 (a-n).(a+n)=404=2.202=202.2 TH1:a-n=2;a+n=202 => a=102;n=100 => a=102;n=-100 loại Vậy n=100 |
17 tháng 1 2016
n2+404=a2
a2-n2=404
(a-n).(a+n)=404=2.202=202.2
TH1:a-n=2;a+n=202
=> a=102;n=100
TH2: a-n=202;a+n=2
=> a=102;n=-100 loại
Vậy n=100
AK
1
LV
0
XO
11 tháng 6 2021
a) Đặt A = 20184n + 20194n + 20204n
= (20184)n + (20194)n + (20204)n
= (....6)n + (....1)n + (....0)n
= (...6) + (...1) + (...0) = (....7)
=> A không là số chính phương
b) Đặt 1995 + n = a2 (1)
2014 + n = b2 (2)
a;b \(\inℤ\)
=> (2004 + n) - (1995 + n) = b2 - a2
=> b2 - a2 = 9
=> b2 - ab + ab - a2 = 9
=> b(b - a) + a(b - a) = 9
=> (b + a)(b - a) = 9
Lập bảng xét các trường hợp
| b - a | 1 | 9 | -1 | -9 | 3 | -3 |
| b + a | 9 | 1 | -9 | -1 | -3 | 3 |
| a | -4 | 4 | 4 | -4 | -3 | 3 |
| b | 5 | 5 | -5 | -5 | 0 | 0 |
Từ a;b tìm được thay vào (1)(2) ta được
n = -1979 ; n = -2014 ;
13 tháng 7 2023
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
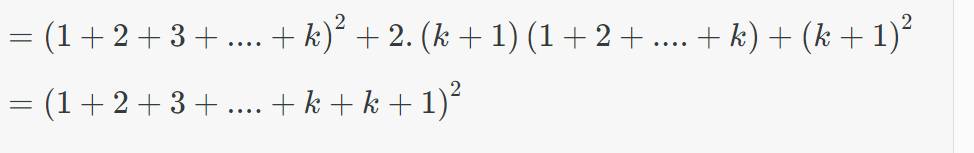
=>ĐPCM
TH
0
Đặt: n2 + 404 = a2 với a2 là số chính phương
=> 404 = a2 - n2
Áp dụng công thức tính hiệu của 2 số chính phương: a2 - n2 = (a + n).(a - n)
và 404 = 202 . 2 => (a + n).(a - n) = 202 . 2
Chọn a + n = 202 và a - n = 2
hoặc a + n = 2 và a - n = 202 (Không xảy ra nên loại)
Khi a + n = 202 và a - n = 2 ta có: a = ( 202 + 2) : 2 = 102
n = ( 202 - 2) : 2 = 100
Lúc đó: 1002 + 404 = 1022
Vậy: Với n = 100 thì n2 + 404 là một số chính phương