P
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PN
3
16 tháng 9 2018
a) ta có: 2300 = (23)100 = 8100
3200 = (32)100 = 9100
=> 8^100 < 9^100 => 2^300 < 3^200
b) ta có: 2109 > 2108
phần c bn ghi thiếu đề r
16 tháng 9 2018
a) ta có: 2300 = (23)100 = 8100
3200 = (32)100 = 9100
=> 8^100 < 9^100 => 2^300 < 3^200
b) ta có: 2109 > 2108
phần c bn ghi thiếu đề r
PV
3
24 tháng 5 2017
\(2110+2109+2108+...+p=21,1.100\\ < =>2110+2109+2108+...+p=2110\\ < =>2110+2109+2108+...+p-2110=0\\ =>p=-2110+1=-2109\)
Mình làm khá ngắn! Mong bạn hiểu bài !
E
0
4 tháng 9 2020
a) \(\frac{8}{9}=1-\frac{1}{9}\)
\(\frac{108}{109}=1-\frac{1}{109}\)
Vì \(\frac{1}{9}>\frac{1}{109}\)
Nên \(1-\frac{1}{9}< 1-\frac{1}{109}\)
Vậy \(\frac{8}{9}< \frac{108}{109}\)
b)
\(\frac{97}{100}=\frac{97\cdot99}{100\cdot99}\)
\(\frac{98}{99}=\frac{98\cdot100}{99\cdot100}\)
\(\Rightarrow\frac{97}{100}< \frac{98}{99}\)
8 tháng 3 2022
TL :
Ko biết thì đừng làm
Nhớ làm hết , chi tiết mới đc 1 SP
HT
XO
16 tháng 8 2020
a) Ta có A = \(\frac{2^{2018}+1}{2^{2019}+1}\)
=> 2A = \(\frac{2^{2019}+2}{2^{2019}+1}=1+\frac{1}{2^{2019}+1}\)
Lại có B = \(\frac{2^{2017}+1}{2^{2018}+1}\)
=> 2B = \(\frac{2^{2018}+2}{2^{2018}+1}=\frac{2^{2018}+1+1}{2^{2018}+1}=1+\frac{1}{2^{2018}+1}\)
Vì \(\frac{1}{2^{2018}+1}>\frac{1}{2^{2019}+1}\Rightarrow1+\frac{1}{2^{2018}+1}>1+\frac{1}{2^{2019}+1}\Rightarrow2B>2A\Rightarrow B>A\)
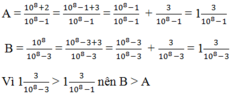
A=108+2108-1108+2108-1=3215
B=108108-3=108105
=> A<B