Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 17/200>17/314
b: 11/54=22/108<22/37
c: 141/893=3/19
159/901=3/17
mà 3/19<3/17
nên 141/893<159/901

a: \(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{45}{4}\cdot\dfrac{2}{15}\)
\(=\dfrac{77}{12}\cdot\dfrac{4}{11}+\dfrac{3}{2}\)
\(=\dfrac{7}{3}+\dfrac{3}{2}=\dfrac{23}{6}\)
b: \(=\left(\dfrac{3}{5}+\dfrac{415}{1000}-\dfrac{3}{200}\right)\cdot\dfrac{8}{3}\cdot\dfrac{1}{4}\)
\(=\dfrac{600+415-15}{1000}\cdot\dfrac{2}{3}=\dfrac{2}{3}\)
c: \(=\dfrac{28}{15}\cdot\dfrac{3}{4}-\left(\dfrac{11}{20}+\dfrac{4}{20}\right)\cdot\dfrac{3}{7}\)
\(=\dfrac{7}{5}-\dfrac{3}{4}\cdot\dfrac{3}{7}=\dfrac{7}{5}-\dfrac{9}{28}=\dfrac{151}{140}\)

a) \(\dfrac{7}{13}\)\(\times\)\(\dfrac{7}{15}\)-\(\dfrac{5}{12}\)\(\times\)\(\dfrac{21}{39}+\dfrac{49}{91}\)\(\times\)\(\dfrac{8}{15}\)
= \(\dfrac{7}{13}\)\(\times\)\(\dfrac{7}{15}\)-\(\dfrac{5}{12}\times\dfrac{7}{13}+\dfrac{7}{13}\times\dfrac{8}{15}\)
= \(\dfrac{7}{13}\left(\dfrac{7}{15}-\dfrac{5}{12}+\dfrac{8}{15}\right)\)
= \(\dfrac{7}{13}\times\dfrac{7}{12}\)
= \(\dfrac{49}{156}\)
b) \(\left(\dfrac{12}{199}+\dfrac{23}{200}-\dfrac{34}{201}\right)\times\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
= \(\left(\dfrac{12}{199}+\dfrac{23}{200}-\dfrac{34}{201}\right)\times0\)
= 0

a: 51/56=1-5/56
61/66=1-5/66
mà -5/56<-5/66
nên 51/56<61/66
b: 41/43<1<172/165
c: \(\dfrac{101}{506}>0>-\dfrac{707}{3534}\)

a, \(A-B=\frac{3}{8^3}+\frac{7}{8^4}-\frac{7}{8^3}-\frac{3}{8^4}==\left(\frac{7}{8^4}-\frac{3}{8^4}\right)-\left(\frac{7}{8^3}-\frac{3}{8^3}\right)=\frac{4}{8^4}-\frac{4}{8^3}< 0\)
Vậy A < B
b, \(A=\frac{10^7+5}{10^7-8}=\frac{10^7-8+13}{10^7-8}=1+\frac{13}{10^7-8}\)
\(B=\frac{10^8+6}{10^8-7}=\frac{10^8-7+13}{10^8-7}=1+\frac{13}{10^8-7}\)
Vì \(10^7-8< 10^8-7\Rightarrow\frac{1}{10^7-8}>\frac{1}{10^8-7}\Rightarrow\frac{13}{10^7-8}>\frac{13}{10^8-7}\Rightarrow A>B\)
c,Áp dụng nếu \(\frac{a}{b}>1\Rightarrow\frac{a}{b}>\frac{a+n}{a+n}\) có:
\(B=\frac{10^{1993}+1}{10^{1992}+1}>\frac{10^{1993}+1+9}{10^{1992}+1+9}=\frac{10^{1993}+10}{10^{1992}+10}=\frac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}=\frac{10^{1992}+1}{10^{1991}+1}=A\)
Vậy A < B

Ta có: \(A=\frac{19^5+2016}{19^5-1}=\frac{19^5-1+2017}{19^5-1}=\frac{19^5-1}{19^5-1}+\frac{2017}{19^5-1}=1+\frac{2017}{19^5-1}\)
\(B=\frac{19^5+2015}{19^5-2}=\frac{19^5-2+2017}{19^5-2}=\frac{19^5-2}{19^5-2}+\frac{2017}{19^5-2}=1+\frac{2017}{19^5-2}\)
Vì \(\frac{2017}{19^5-1}< \frac{2017}{19^5-2}\Rightarrow1+\frac{2017}{19^5-1}< 1+\frac{2017}{19^5-2}\Rightarrow A< B\)
Vậy A < B

\(A=\frac{19^5+2016}{19^5-1}=\frac{\left(19^5-1\right)+2017}{19^5-1}=1+\frac{2017}{19^5-1}\)
\(B=\frac{19^5+2015}{19^5-2}=\frac{\left(19^5-2\right)+2017}{19^5-2}=1+\frac{2017}{19^5-2}\)
Vì \(19^5-1>19^5-2\) nên \(\frac{2017}{19^5-1}< \frac{2}{19^5-2}\)
\(\Rightarrow1+\frac{2017}{19^5-1}< 1+\frac{2017}{19^5-2}\)
Vậy \(A< B\)

a) \(\dfrac{3}{5}+0,145-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{145}{1000}-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{29}{200}-\dfrac{1}{200}\)
\(=\dfrac{120}{200}+\dfrac{29}{200}-\dfrac{1}{200}\)
\(=\dfrac{148}{200}\)
\(=\dfrac{37}{50}\)
b) \(\left(31\dfrac{6}{13}+5\dfrac{9}{41}\right)-36\dfrac{6}{13}\)
\(=31\dfrac{6}{13}+5\dfrac{9}{41}-36\dfrac{6}{13}\)
\(=\left(31\dfrac{6}{13}-36\dfrac{6}{13}\right)+5\dfrac{5}{41}\)
\(=\left(-5\right)+5\dfrac{5}{41}\)
\(=0\dfrac{5}{41}\)
\(=\dfrac{5}{41}\)
c) \(5.2\dfrac{1}{7}+5.7\dfrac{6}{7}\)
\(=5\left(2\dfrac{1}{7}+7\dfrac{6}{7}\right)\)
\(=5\left(9+\dfrac{1}{7}+\dfrac{6}{7}\right)\)
\(=5\left(9+1\right)\)
\(=5.10\)
\(=50\)
a) \(\dfrac{3}{5}+0,415-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{83}{200}-\dfrac{1}{200}\\ =\dfrac{120}{200}+\dfrac{83}{200}-\dfrac{1}{200}\\ =\dfrac{120+83-1}{200}=\dfrac{202}{200}=\dfrac{101}{100}\)
b)\(\left(31\dfrac{6}{13}+5\dfrac{9}{41}\right)-36\dfrac{6}{13}\)
\(=\left(\dfrac{409}{13}+\dfrac{214}{41}\right)-\dfrac{474}{13}\)
\(=\dfrac{19551}{533}-\dfrac{474}{13}=\dfrac{9}{41}\)
c)\(5.2\dfrac{1}{7}+5.7\dfrac{6}{7}\)
\(=5.\dfrac{15}{7}+5.\dfrac{55}{7}\\ =5\left(\dfrac{15}{7}+\dfrac{55}{7}\right)\\ =5.10=50\)

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

\(S^2=\left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\\ \text{Ta có:}\\ \dfrac{1}{2}< \dfrac{2}{3}\\ \dfrac{3}{4}< \dfrac{4}{5}\\ \dfrac{5}{6}< \dfrac{6}{7}\\ ...\\ \dfrac{199}{200}< \dfrac{200}{201}\\ \Rightarrow S^2< \left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\left(\dfrac{2}{3}\cdot\dfrac{4}{5}\cdot\dfrac{6}{7}\cdot...\cdot\dfrac{200}{201}\right)\\ \Leftrightarrow S^2< \dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{199}{200}\cdot\dfrac{200}{201}\\ \Leftrightarrow S^2< \dfrac{1\cdot2\cdot3\cdot...\cdot200}{2\cdot3\cdot4\cdot...\cdot201}\\ \Leftrightarrow S^2< \dfrac{1}{201}< \dfrac{1}{200}\)
Vậy ...
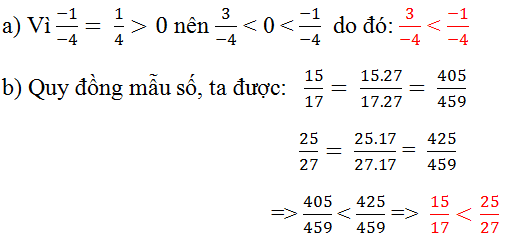
\(\dfrac{1}{2^{500}}=\dfrac{1}{\left(2^5\right)^{100}}=\dfrac{1}{32^{100}}\\ \dfrac{1}{5^{200}}=\dfrac{1}{\left(5^2\right)^{100}}=\dfrac{1}{25^{100}}\)
mà `32^(100)>25^(100)`
nên \(\dfrac{1}{2^{500}}>\dfrac{1}{5^{200}}\)