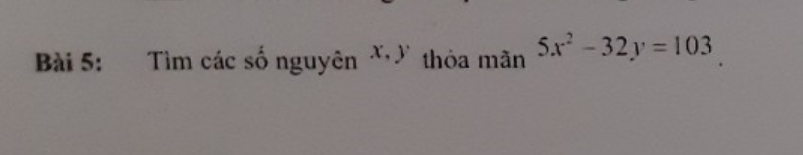Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(25.\left(x+3\right)=250\)
\(x+3=250:25\)
\(x+3=10\)
\(x=10-3\)
\(\Rightarrow x=7\)

id của mik 88461550
còn câu hỏi thì mik ko bt nhé mik mới lớp4
nick là ri nhé
Ta thấy mẫu số ở PS A = mẫu số PS B nên ta xét ở tử số của 2 số.
2020+201<2020+2019 nên PS B lớn hơn
Mik ko chơi mini world nha k mik vs

\(xy=x-y+3\)
\(\Leftrightarrow xy-x+y=3\)
\(\Leftrightarrow x\left(y-1\right)+\left(y-1\right)=2\)
\(\Leftrightarrow\left(x+1\right)\left(y-1\right)=2\)
\(\Leftrightarrow x+1;y-1\inƯ\left(2\right)\)
Ta có: \(Ư\left(2\right)=\left\{\pm1;\pm2\right\}\)
Lập bảng:
| x + 1 | -1 | 1 | -2 | 2 |
| x | -2 | 0 | -3 | 1 |
| y - 1 | -2 | 2 | -1 | 1 |
| y | -1 | 3 | 0 | 2 |
| KL | tm | tm | tm | tm |
Vậy các cặp số nguyên (x; y) thỏa mãn là (-2; -1); (0;3); (-3; 0) và (1; 2)

\(A=\frac{19^{30}+5}{19^{31}+5}=>19A=\frac{19^{31}+95}{19^{31}+5}=1+\frac{90}{19^{31}+5}\left(1\right)\)
\(B=\frac{19^{31}+5}{19^{32}+5}=>19B=\frac{19^{32}+95}{19^{32}+5}=1+\frac{90}{19^{32}+5}\left(2\right)\)
từ (1) and (2)
=>19A>19B
=>A>B
Ta có:
19A=19^31+95/19^31+5
19A= (19^31+5)+90/19^31+5
19A=1+90/19^31+5
19B=19^32+95/19^32+5
19B=(19^32+5)+90/19^32+5
19B=1+90/19^32+5
Vì: 90/19^31+5>90/19^31+5 nên 19A>19B hay A>B

Ta có:
\(C=\dfrac{2n-3}{n-2}=\dfrac{2n-4+1}{n-2}=2+\dfrac{1}{n-2}\)
\(C\in Z\Leftrightarrow\dfrac{1}{n-2}\in Z\Leftrightarrow n-2\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(\Rightarrow...\)

a) 41. 36+ 59. 90 + 41. 84 + 59. 30
= 41 . (36 + 84) + 59 . (90 + 30)
= 41 . 120 + 59 . 120
= 120 . ( 41 + 59 )
= 120 . 100
= 12000
b) 4. 51 . 7 + 2 . 86 .7 + 6 . 4 . 7
= 28 . 51 + 2 . 43 . 2 . 7 + 6 . 4 . 7
= 28 . 51 + 28 . 43 + 28 . 6
= 28 . ( 51 + 43 + 6 )
= 28 . 100
= 2800
c) ( 4.7 ) . 5 + ( 4.7 ) . 43 + ( 4.7) - 6
= 28 . 5 + 28 .43 + 28 - 6
= 28 . (5 + 43 + 1) - 6
= 28 . 49 - 6
= 1372 - 6
= 1366.
d) 53 . 39 + 47 . 39 - 53 . 21 - 47 . 21
= 53 . (39 - 21) + 47. (39 - 21)
= (39 - 21) . ( 53 + 47 )
= 18 . 100
= 1800.

Do 103 là số nguyên tố lẻ và 32y chẵn nên \(5x^2\) lẻ
Do đó \(x^2\) lẻ
\(\Leftrightarrow x^2:4\) dư 1
Mà \(32y⋮4\Leftrightarrow5x^2-32y:4\) dư 1
Mà \(103:4\) dư 3 nên PT vô nghiệm

\(A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^8}\)
\(3A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^7}\)
\(3A-A=\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^7}\right)-\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^8}\right)\)
\(2A=1-\frac{1}{3^8}\)
\(A=\frac{1}{2}-\frac{1}{2.3^8}\)