Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử z = x + yi (x, y ∈ R), khi đó số phức z được biểu diễn bởi điểm M(x, y) trên mặt phẳng tọa độ Oxy.
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ x ≥ 1, tung độ y tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng -1 có điểm biểu diễn ở hình 71.a (SGK)
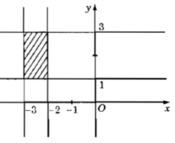
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ y ∈ [1, 2], hoành độ x tùy ý.
Vậy số phức có phần ảo thuộc đoạn [-1, 2]
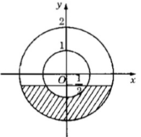
c) Trên hình 71.c (SGK), hình biểu diễn z có hoành độ x ∈ [-1, 1] và x2 + y2 ≤ 4 (vì |z| ≤ 4.
Vậy số phực có phần thực thuộc đoạn [-1, 1] và môdun không vượt quá 2.


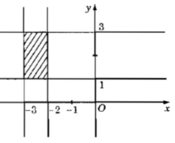
a) Phần thực của z thuộc đoạn [-3; -2] trên trục Ox; phần ảo của z thuộc đoạn [1; 3] trên trục Oy.
b) Phần ảo của z nhỏ hơn hoặc bằng -0,5, 1 ≤ |z| ≤ 2.

Phần thực của z thuộc đoạn [-3; -2] trên trục Ox; phần ảo của z thuộc đoạn [1; 3] trên trục Oy


Chọn A.
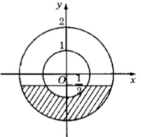
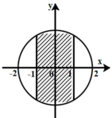
+ Từ hình biểu diễn ta thấy tập hợp các điểm M(a; b) biểu diễn số phức z trong phần gạch chéo đều thuộc đường tròn tâm O(0;0) và bán kính bằng 2; ngoài ra -1 ≤ a ≤ 1.
+ Vậy M(a; b) là điểm biểu diễn của các số phức z = a + bi có mô đun nhỏ hơn hoặc bằng 2 và có phần thực thuộc đoạn [-1;1].
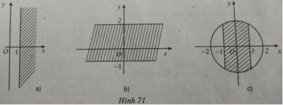


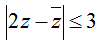
a) Mỗi số phức z = a + bi có điểm biểu diễn trong miền gạch sọc ở hình a phải thỏa mãn điều kiện: phần thực a ≥ 1 ( phần ảo b bất kì).
b) Số phức z = a + bi có điểm biểu diễn trong miền gạch sọc ở hình b phải thỏa mãn điều kiện : phần ảo b ∈ [-1;2] ( phần thực a bất kì).
c) Số phức z = a + bi có điểm biểu diễn trong miền gạch sọc ở hình c phải thỏa mãn 2 điều kiện:
+ Mô đun của z là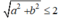
+ Phần thực a ∈ [-1; 1]