NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
1
TN
25 tháng 4 2016
đặt tử là A,ta có:
2A=2(1+2+22+23+...+22008)
2A=2*1+2*2+2*22+...+2*22008
2A=2+22+23+...+22009
2A-A=(2+22+23+...+22009)-(1+2+22+...+22008)
A=22009-1
thay A vào tử số ta được \(B=\frac{2^{2009}-1}{1-2^{2009}}=-1\)
RM
24 tháng 7 2017
\(A=2^0+2^1+2^2\)\(+2^3+...+\)\(2^{50}\)
\(2A=2+2^2+2^3+...+2^{51}\)
\(2A-A=A=2^{51}-2^0\)
\(B=5+5^2+5^3+...+5^{99}+5^{100}\)
\(5B=5^2+5^3+5^4+...+5^{100}+5^{101}\)
\(5B-B=4B=5^{101}-5\)
\(B=\frac{5^{101}-5}{4}\)
\(C=3-3^2+3^3-3^4+...+\)\(3^{2007}-3^{2008}+3^{2009}-3^{2010}\)
\(3C=3^2-3^3+3^4-3^5+...-3^{2008}+3^{2009}-3^{2010}+3^{2011}\)
\(3C+C=4C=3^{2011}+3\)
\(C=\frac{3^{2011}+3}{4}\)
\(S_{100}=5+5\times9+5\times9^2+5\times9^3+...+5\times9^{99}\)
\(S_{100}=5\times\left(1+9+9^2+9^3+...+9^{99}\right)\)
\(9S_{100}=5\times\left(9+9^2+9^3+...+9^{99}+9^{100}\right)\)
\(9S_{100}-S_{100}=8S_{100}=5\times\left(9^{100}-1\right)\)
\(S_{100}=\frac{5\times\left(9^{100}-1\right)}{8}\)
24 tháng 10 2023
A=20+21+22+23+...++23+...+250250
2�=2+22+23+...+2512A=2+22+23+...+251
2�−�=�=251−202A−A=A=251−20
�=5+52+53+...+599+5100B=5+52+53+...+599+5100
5�=52+53+54+...+5100+51015B=52+53+54+...+5100+5101
5�−�=4�=5101−55B−B=4B=5101−5
�=5101−54B=45101−5
�=3−32+33−34+...+C=3−32+33−34+...+32007−32008+32009−3201032007−32008+32009−32010
3�=32−33+34−35+...−32008+32009−32010+320113C=32−33+34−35+...−32008+32009−32010+32011
3�+�=4�=32011+33C+C=4C=32011+3
�=32011+34C=432011+3
�100=5+5×9+5×92+5×93+...+5×999S100=5+5×9+5×92+5×93+...+5×999
�100=5×(1+9+92+93+...+999)S100=5×(1+9+92+93+...+999)
9�100=5×(9+92+93+...+999+9100)9S100=5×(9+92+93+...+999+9100)
9�100−�100=8�100=5×(9100−1)9S100−S100=8S100=5×(9100−1)
�100=5×(9100−1)8S100=85×(9100−1)
HL
0
KS
13 tháng 5 2022
cop bài trên mạng ko có càu này mik làm r rồi chụp lại nhé ;-;
KS
13 tháng 5 2022
a)
`A = 1 + 2 + 2^2 + .....+2^2015`
=>`2A = 2 + 2^2 + 2^3 + ... + 2^2016`
=> `2A - A= (2 + 2^2 + 2^3 + ... + 2^2016)-(1 + 2 + 2^2 + ... + 2^2015)`
=> `A = 2^2016 - 1`
b) `4^2008 = (2^2)^2008 = 2^4016 > 2^2016 - 1`
ND
3
24 tháng 12 2017
A = 1 + 2 + 22 + 23 + 24 + ... + 2100
2A = 2 + 22 + 23 + 24 + 25 + ... + 2101
2A - A = ( 2 + 22 + 23 + 24 + 25 + ... + 2101 ) - ( 1 + 2 + 22 + 23 + 24 + ... + 2100 )
A = 2101 - 1
T
20 tháng 10 2018
Câu 1:
\(A=4+4^2+4^3+.....+4^{2008}\)
\(\Rightarrow4A=4^2+4^3+4^4+...+4^{2009}\)
\(\Rightarrow4A-A=\left(4^2+4^3+4^4+....+4^{2009}\right)-\left(4+4^2+4^3+....+4^{2008}\right)\)
\(\Rightarrow3A=4^{2009}-4\)
\(\Rightarrow A=\frac{4^{2009}-4}{3}\)
Câu 2:
Đặt \(B=A+1=1+4+4^2+4^3+4^4+....+4^{2008}\)
\(=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...+\left(4^{2006}+4^{2007}+4^{2008}\right)\)
\(=21+4^3\left(1+4+4^2\right)+...+4^{2006}\left(1+4+4^2\right)\)
\(=21+4^3\cdot21+...+4^{2006}\cdot21\)
\(=21\left(1+4^3+...+4^{2006}\right)\)
\(\Rightarrow B⋮21\)
\(\Rightarrow A=B-1\)Không chia hết cho 21
DL
1
7 tháng 9 2017
Ta có M = 1 - 2 + 22 - 23 + ... + 22008
=> 2M = 2 - 22 + 23 + ... - 22008 + 22009
=> 2M + M = 22009 + 1
=> 3M = 22009 + 1
=> \(M=\frac{2^{2009}+1}{3}\)
PT
0
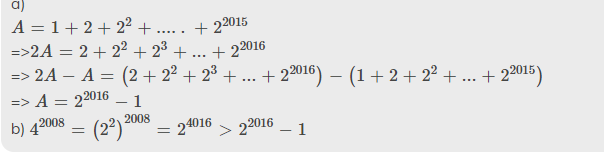
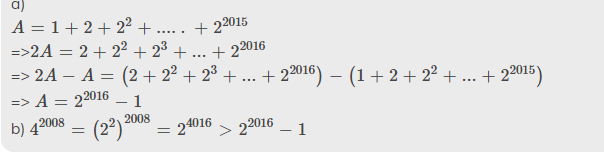
Lời giải:
$M=1-2+2^2-2^3+...+2^{2008}$
$2M=2-2^2+2^3-2^4+...+2^{2009}$
$M+2M=(1-2+2^2-2^3+...+2^{2008})+(2-2^2+2^3-2^4+...+2^{2009})$
$3M=2^{2009}+1$
$M=\frac{2^{2009}+1}{3}$