
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\frac{3\sqrt{x}+1}{x+2\sqrt{x}-3}-\frac{2}{\sqrt{x}+3}\) ĐK : \(x\ge0;x\ne1\)
\(=\frac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\frac{2}{\sqrt{x}+3}\)
\(=\frac{3\sqrt{x}+1-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\frac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\frac{1}{\sqrt{x}-1}\)
\(=\frac{3\sqrt{x}+1}{\left(\sqrt{x}+3\right)\cdot\left(\sqrt{x}-1\right)}-\frac{2}{\sqrt{x}+3}\)
\(=\frac{3\sqrt{x}+1-2\cdot\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\cdot\left(\sqrt{x}-1\right)}\)
\(=\frac{3\sqrt{x}+1-2\sqrt{x}+2}{\left(\sqrt{x}+3\right)\cdot\left(\sqrt{x}-1\right)}\)
\(=\frac{\sqrt{x}+3}{\left(\sqrt{x}+3\right)\cdot\left(\sqrt{x}-1\right)}\)
\(=\frac{1}{\sqrt{x}-1}\)

\(B=\frac{3\sqrt{x}+1}{x+2\sqrt{x}-3}-\frac{2}{\sqrt{x}+3}\)
\(=\frac{3\sqrt{x}+1-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\frac{3\sqrt{x}+1-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\frac{1}{\sqrt{x}-1}\)


a: \(=\dfrac{x-\sqrt{x}-x-2\sqrt{x}-1-2\sqrt{x}-4}{x-1}\)
\(=\dfrac{-5\sqrt{x}-5}{x-1}=\dfrac{-5}{\sqrt{x}-1}\)
b: \(=\dfrac{5x+10\sqrt{x}+\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)-6x}{x-4}\)
\(=\dfrac{-x+10\sqrt{x}+x-5\sqrt{x}+6}{x-4}\)
\(=\dfrac{5\sqrt{x}+6}{x-4}\)

Với \(x\ge0;x\ne\pm16\)
\(B=\left(\frac{\sqrt{x}}{\sqrt{x}+4}+\frac{4}{\sqrt{x}-4}\right):\frac{x+16}{\sqrt{x}+2}\)
\(=\left(\frac{x-4\sqrt{x}+4\sqrt{x}+16}{x-16}\right):\frac{x+16}{\sqrt{x}-2}=\frac{\sqrt{x}-2}{x-16}\)

\(\left(\sqrt{75}+\sqrt{243}-\sqrt{48}\right):\sqrt{3}\)
\(=\sqrt{75}:\sqrt{3}+\sqrt{243}:\sqrt{3}-\sqrt{48}:\sqrt{3}\)
\(=\sqrt{75:3}+\sqrt{243:3}-\sqrt{48:3}\)
\(=\sqrt{25}+\sqrt{81}-\sqrt{16}\)
\(=5+9-4=10\)
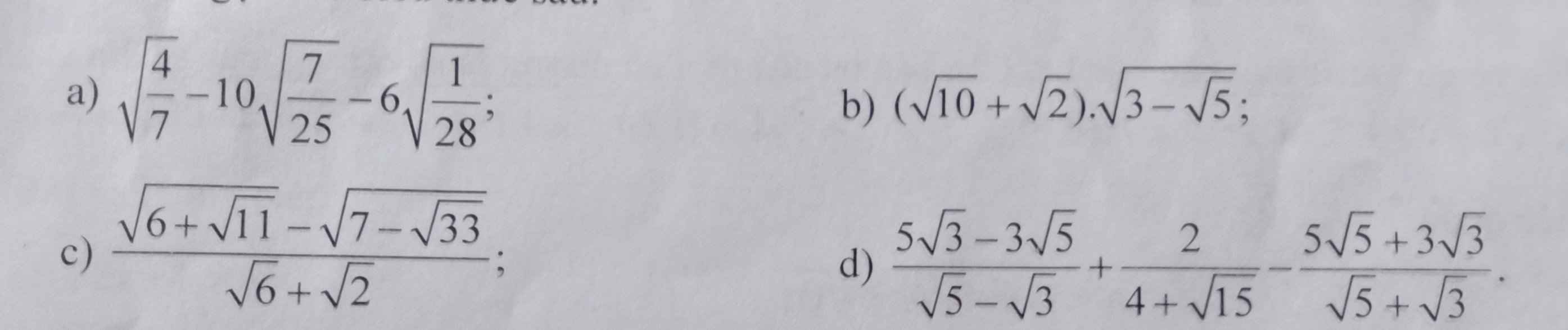 rút gọn giúp mình vs ạ
rút gọn giúp mình vs ạ 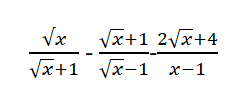
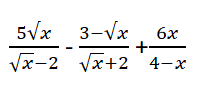

Với `x > 0,x \ne 1` có:
`1/[x+\sqrt{x}]+[2\sqrt{x}]/[x-1]-1/[x-\sqrt{x}]`
`=[\sqrt{x}-1+2x-\sqrt{x}-1]/[\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+1)]`
`=[2x-2]/[\sqrt{x}(x-1)]`
`=[2(x-1)]/[\sqrt{x}(x-1)]`
`=2/\sqrt{x}`