Chương trình khuyến mại lớn nhất năm: Lì xì đầu xuân - Nhân đôi gói VIP, xem ngay!

Bộ GD&ĐT cấm dạy thêm: Giải pháp nào dành cho nhà trường và giáo viên?

K
Khách

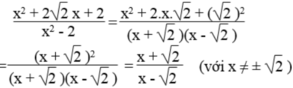
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
CD
Cỏ dại
9 tháng 6 2019 - olm

Rút gọn các biểu thức :

\(\frac{\sqrt{x^2}+\sqrt{4-4x+x^2+1}}{2x-1}\) với x > 2.
#Hỏi cộng đồng OLM #Toán lớp 9
1
G
ღᏠᎮღ🆃🆄ấ🅽ঔ 🅽🅰🅼ঌ❄๖ۣۜ
9 tháng 6 2019

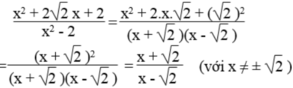
\(\frac{\sqrt{x^2}+\sqrt{4-4x+x^2+1}}{2x-1}\)

\(=\frac{x+2-2\sqrt{x}+1}{2x-1}\)

\(=1+\frac{4-2\sqrt{x}}{2x-1}\)

em lớp 8 chỉ làm được thế thôi

Đúng(0)
HK
Hoàng Kiệt
25 tháng 11 2016 - olm
1 Cho biểu thức B=\(\frac{x\sqrt{x}-4x-\sqrt{x}+4}{2x\sqrt{x}-14x+28\sqrt{x}-16}\)a) Tìm x để A có nghĩa, từ đó rút gọn biểu thức Bb) Tìm các giá trị nguyên của x để biểu thức B nhận giá trị nguyên2 cho biểu thức P=\(\left(\frac{4\sqrt{x}}{2+\sqrt{x}}+\frac{8x}{4-x}\right)\div\left(\frac{\sqrt{x}-1}{x-2\sqrt{x}}-\frac{2}{\sqrt{x}}\right)\)a) Rút gọn Pb) Tìm giá trị của x để P=-13 Rút gọn...
Đọc tiếp

1 Cho biểu thức B=\(\frac{x\sqrt{x}-4x-\sqrt{x}+4}{2x\sqrt{x}-14x+28\sqrt{x}-16}\)

a) Tìm x để A có nghĩa, từ đó rút gọn biểu thức B

b) Tìm các giá trị nguyên của x để biểu thức B nhận giá trị nguyên

2 cho biểu thức P=\(\left(\frac{4\sqrt{x}}{2+\sqrt{x}}+\frac{8x}{4-x}\right)\div\left(\frac{\sqrt{x}-1}{x-2\sqrt{x}}-\frac{2}{\sqrt{x}}\right)\)

a) Rút gọn P

b) Tìm giá trị của x để P=-1

3 Rút gọn Q=\(\frac{2\sqrt{4-\sqrt{5+21+\sqrt{80}}}}{\sqrt{10}-\sqrt{2}}\)
#Hỏi cộng đồng OLM #Toán lớp 9
0
SG
Sách Giáo Khoa
23 tháng 4 2017

Rút gọn các phân tử :

a) \(\dfrac{x^2-5}{x+\sqrt{5}}\) ( với \(x\ne-\sqrt{5}\))

b) \(\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}\) (với \(x\ne\pm\sqrt{2}\) )
#Hỏi cộng đồng OLM #Toán lớp 9
1
DH
đỗ hải anh
2 tháng 5 2017

a) \(\dfrac{x^2-5}{x+\sqrt{5}}\)(với x khác -\(\sqrt{5}\)) =\(\dfrac{\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)}{x+\sqrt{5}}\) = x-\(\sqrt{5}\) vậy \(\dfrac{x^2-5}{x+\sqrt{5}}\) = x-\(\sqrt{5}\) với x khác -\(\sqrt{5}\) b) \(\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}\) ( với x khác +-\(\sqrt{2}\) ) = \(\dfrac{\left(x+\sqrt{2}\right)^2}{\left(x+\sqrt{2}\right)\left(x-\sqrt{2}\right)}\) =\(\dfrac{x+\sqrt{2}}{x-\sqrt{2}}\) vậy \(\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}\) =\(\dfrac{x+\sqrt{2}}{x-\sqrt{2}}\) với x khác +-\(\sqrt{2}\)

Đúng(0)
F
fairy
27 tháng 5 2017 - olm

Rút gọn biểu thức:\(\frac{x^2+5x+6+x\sqrt{9-x^2}}{3x-x^2+\left(x+2\right)\sqrt{9-x^2}}\)
#Hỏi cộng đồng OLM #Toán lớp 9
1
HT
Hoàng Thanh Tuấn
28 tháng 5 2017

\(=\frac{\left(x^2+5x+6\right)+x\sqrt{9-x^2}}{\left(3x-x^2\right)+\left(2+x\right)\sqrt{9-x^2}}\)

\(=\frac{\left(x+2\right)\left(3+x\right)+x\sqrt{\left(3+x\right)\left(3-x\right)}}{x\left(3-x\right)+\left(x+2\right)\sqrt{\left(3+x\right)\left(3-x\right)}}\) nhóm nhân tử chung

\(=\frac{\sqrt{3+x}\left(\left(x+2\right)\sqrt{3+x}+x\sqrt{3-x}\right)}{\sqrt{3-x}\left(x\sqrt{3-x}+\left(x+2\right)\sqrt{3+x}\right)}\)rồi rút gọn được

\(=\frac{\sqrt{3+x}}{\sqrt{3-x}}\)

Đúng(0)
NM
Nguyễn Mai
20 tháng 11 2019 - olm

Cho biểu thức \(A=\frac{\sqrt{x+2-4\sqrt{x-2}}+\sqrt{x+2+4\sqrt{x-2}}}{\sqrt{\frac{4}{x^2}-\frac{4}{x}+1}}\)

a, Rút gọn biểu thức A

b, Tìm các số nguyên x để A là một số nguyên
#Hỏi cộng đồng OLM #Toán lớp 9
0
NK
nguyen khai
20 tháng 6 2017 - olm

rút gọn biểu thức

\(\frac{\sqrt{2x+2\sqrt{x^2+4}}}{\sqrt{x^2-4}+x+2}\)
#Hỏi cộng đồng OLM #Toán lớp 9
0
PM
Phạm Minh Thành
14 tháng 7 2018 - olm
Các bạn giải chi tiết giùm mk nhé . Xin cảm ơnBài 1 : Rút gọn A=\(\sqrt[3]{\frac{x^3-3x+\left(x^2-1\right)\sqrt{x^2-4}}{2}}\) + \(\sqrt[3]{\frac{x^3-3x-\left(x^2-1\right)\sqrt{x^2-4}}{2}}\) Bài 2 : Cho biểu thức : P= \(\frac{x^2-4x-\left(x-1\right)\sqrt{x^2-9}+3}{x^2+4x-\left(x+1\right)\sqrt{x^2-9}+3}\)* \(\sqrt{\frac{x+3}{x-3}}\)với x>3a> Rút gọn biểu thức Pb> Tìm giá trị lớn nhất của...
Đọc tiếp

Các bạn giải chi tiết giùm mk nhé . Xin cảm ơn

Bài 1 : Rút gọn A=\(\sqrt[3]{\frac{x^3-3x+\left(x^2-1\right)\sqrt{x^2-4}}{2}}\) + \(\sqrt[3]{\frac{x^3-3x-\left(x^2-1\right)\sqrt{x^2-4}}{2}}\)

 

Bài 2 : Cho biểu thức : P= \(\frac{x^2-4x-\left(x-1\right)\sqrt{x^2-9}+3}{x^2+4x-\left(x+1\right)\sqrt{x^2-9}+3}\)* \(\sqrt{\frac{x+3}{x-3}}\)với x>3

a> Rút gọn biểu thức P

b> Tìm giá trị lớn nhất của M= \(\frac{2}{P\left(x\right)}+\frac{1-x}{2016}\)

 
#Hỏi cộng đồng OLM #Toán lớp 9
0
MT
Minh Triều
6 tháng 8 2015 - olm

Rút gọn biểu thức:

\(B=\sqrt{x^2+\frac{1}{x^2}-2}-\sqrt{x^2+\frac{1}{x^2}+2}\)
#Hỏi cộng đồng OLM #Toán lớp 9
2
DD
Đào Đức Mạnh
6 tháng 8 2015

\(B=\sqrt{x^2+\frac{1}{x^2}-2}-\sqrt{x^2+\frac{1}{x}+2}=\sqrt{\left(x-\frac{1}{x}\right)^2}-\sqrt{\left(x+\frac{1}{x}\right)^2}=x-\frac{1}{x}-x-\frac{1}{x}=-\frac{2}{x}\)

 

Đúng(0)
TT
Trần Thị Loan
6 tháng 8 2015

\(B=\sqrt{\left(x-\frac{1}{x}\right)^2}-\sqrt{\left(x+\frac{1}{x}\right)^2}=\left|x-\frac{1}{x}\right|-\left|x+\frac{1}{x}\right|=\frac{\left|x^2-1\right|}{\left|x\right|}-\frac{x^2+1}{\left|x\right|}=\frac{\left|x^2-1\right|-\left(x^2+1\right)}{\left|x\right|}\)

x2 - 1 > 0 <=> (x-1).(x+1) > 0 => x + 1 < 0 hoặc x - 1> 0  <=> x <-1 hoặc x > 1

Vậy 

+) Khi x < -1 => B = \(\frac{x^2-1-\left(x^2+1\right)}{-x}=\frac{2}{x}\)

+) Khi  -1< x< 0 thì B =  \(\frac{-\left(x^2-1\right)-\left(x^2+1\right)}{-x}=\frac{-2x^2}{-x}=2x\)

+) Khi 0 < x < 1 thì B =  \(\frac{-\left(x^2-1\right)-\left(x^2+1\right)}{x}=\frac{-2x^2}{x}=-2x\)

+) Khi x  > 1 thì B =  \(\frac{\left(x^2-1\right)-\left(x^2+1\right)}{x}=\frac{-2}{x}\)

 

Đúng(0)
NT
nguyen thao
25 tháng 7 2020 - olm
Mik đag cần gấp giải giúp vs Cho biểu thức B=\((\frac{\sqrt{x}+1}{\sqrt{x}+2}-\frac{2\sqrt{x}}{\sqrt{x}+2}+\frac{5\sqrt{x}+2}{4-x}):\frac{3\sqrt{x-x}}{x+\sqrt{x}+4}\)a) Rút gọn Bb) Tìm x để B=2c)Tìm x để B nhận giá trị âmCho biểu thức P=\((\frac{x}{x\sqrt{x}-4\sqrt{x}}-\frac{6}{3\sqrt{x}-6}+\frac{1}{\sqrt{x}+2}):(\frac{\sqrt{x}-2+10-x}{\sqrt{x}+2})\)a) Rút gọn Pb)Tìm các giá trị nguyên của x để biểu thức Q=\((-\sqrt{x}-1)\)P nhận đc giá...
Đọc tiếp

Mik đag cần gấp giải giúp vs 

Cho biểu thức B=\((\frac{\sqrt{x}+1}{\sqrt{x}+2}-\frac{2\sqrt{x}}{\sqrt{x}+2}+\frac{5\sqrt{x}+2}{4-x}):\frac{3\sqrt{x-x}}{x+\sqrt{x}+4}\)

a) Rút gọn B

b) Tìm x để B=2

c)Tìm x để B nhận giá trị âm

Cho biểu thức P=\((\frac{x}{x\sqrt{x}-4\sqrt{x}}-\frac{6}{3\sqrt{x}-6}+\frac{1}{\sqrt{x}+2}):(\frac{\sqrt{x}-2+10-x}{\sqrt{x}+2})\)

a) Rút gọn P

b)Tìm các giá trị nguyên của x để biểu thức Q=\((-\sqrt{x}-1)\)P nhận đc giá trị nguyên
#Hỏi cộng đồng OLM #Toán lớp 9
0
NM
Nguyễn Minh Khánh
29 tháng 6 2019 - olm

\(A=\frac{x+\sqrt{x^2-2x}}{x-\sqrt{x^2-2x}}-\frac{x-\sqrt{x^2-2x}}{x+\sqrt{x^2-2x}}\)

rút gọn biểu thức
#Hỏi cộng đồng OLM #Toán lớp 9
1
TN
Thanh nguyen
29 tháng 6 2019

\(A=\frac{\left(x+\sqrt{x^2-2x}\right)^2-\left(x-\sqrt{x^2-2x}\right)^2}{\left(x-\sqrt{x^2-2x}\right)\left(x+\sqrt{x^2-2x}\right)}\)

      \(=\frac{2x\times2\sqrt{x^2-2x}}{2x}=2\sqrt{x^2-2x}\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP