K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
Ta lập bảng thống kê cho dữ liệu được biểu diễn trong biểu đồ trên như sau:
Loại vé | 100 000 đồng | 150 000 đồng | 200 000 đồng |
Số lượng (nghìn vé) | 10 | 20 | 5 |
Để biểu diễn dữ liệu Bảng 5.1, ta nên chọn biểu đồ tranh.
Ta chọn mỗi biểu tượng biểu diễn cho 5 nghìn vé.
Khi đó, số biểu tượng biểu tượng cần biểu diễn số vé 100 000 đồng là:
10 : 5 = 2 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 150 000 đồng là:
20 : 5 = 4 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 200 000 đồng là:
5 : 5 = 1 (biểu tượng)
Ta vẽ biểu đồ tranh như sau:
Loại vé 100 000 đồng | ☺ ☺ |
Loại vé 150 000 đồng | ☺ ☺ ☺ ☺ |
Loại vé 200 000 đồng | ☺ |
(Mỗi ☺ ứng với 5 nghìn vé)
QT
1
11 tháng 9 2023
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
Bạn tròn làm thế là sai. Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ không phải chia cho nhân tử chung của cả tử và mẫu.
trong công cụ 
để kiểm tra trung điểm AC và BD có trùng nhau không.
QT
Quoc Tran Anh Le
Giáo viên
14 tháng 1 2024
a) Dùng 
trong công cụ 
để kiểm tra trung điểm AC và BD, ta thấy trung điểm AC và BD trùng nhau.
b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm B, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Chọn điểm C bất kỳ nằm trên đường tròn tâm B.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm C, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột đường tròn tâm A và đường tròn C.
Chọn công cụ 
để nối B với C, C với D, D với A.
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.
QT
2
10 tháng 9 2023
\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
10 tháng 9 2023
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)
+Dùng +trong+công+cụ +để+kiểm+tra+trung+điểm+AC+và+BD+có+trùng+nhau+không.b)+Lưu+hình+vẽ+ở+HĐ2+thành+tệp+hbh.png.c)+Tương+tự,+hãy+vẽ+một+hình+thoi+ABCD+có+cạnh+4+cm.){kind=link}
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)
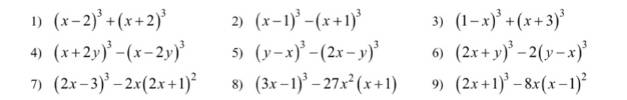
1: =x^3-6x^2+12x-8+x^3+6x^2+12x-8
=2x^3+24x
2: =x^3-3x^2+3x-1-x^3-3x^2-3x-1
=-6x^2-2
3: =1-3x+3x^2-x^3+x^3+9x^2+27x+27
=24x+12x^2+28
4: =x^3+6x^2y+12xy^2+8y^3-x^3+6x^2y-12xy^2+8y^3
=12x^2y+16y^3
5: =y^3-3y^2x+3yx^2-x^3-8x^3+12x^2y-6xy^2+y^3
=2y^3-9xy^2+15x^2y-9x^3
7: =8x^3-36x^2+54x-27-2x(4x^2+4x+1)
=8x^3-36x^2+54x-27-8x^3-8x^2-2x
=-44x^2+52x-27
8: =27x^3-27x^2+9x-1-27x^3-27x^2
=-54x^2+9x-1