Rút gọn các biểu thức: 15 200 - 3 450...

Rút gọn các biểu thức: 15 200...

SG

Sách Giáo Khoa

25 tháng 4 2017

Rút gọn các biểu thức :

a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\)

b) \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)

c) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

MP

Mysterious Person

25 tháng 6 2017

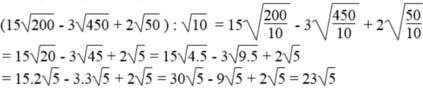
a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\)

= \(2-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\)

\(2-\sqrt{3}+\sqrt{3}-1\) = \(1\)

b) \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)

= \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(3-2\sqrt{6}\right)^2}\)

= \(3-\sqrt{6}+2\sqrt{6}-3\) = \(\sqrt{6}\)

c) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)

= \(\dfrac{15\sqrt{200}}{\sqrt{10}}-\dfrac{3\sqrt{450}}{\sqrt{10}}+\dfrac{2\sqrt{50}}{\sqrt{10}}\)

= \(15\sqrt{20}-3\sqrt{45}+2\sqrt{5}\)

= \(30\sqrt{5}-9\sqrt{5}+2\sqrt{5}\) = \(23\sqrt{5}\)

Đúng(0)

TN

Thai Nguyen

6 tháng 7 2018 - olm

Rút gọn các biểu thức sau:

a) \(0,2\sqrt{\left(-10\right)^2.3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\) b) \(\left(15\sqrt{50}+5\sqrt{200}-3\sqrt{450}\right):\sqrt{10}\)

c) \(\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right):\sqrt{6}\) d) \(\frac{\sqrt{5+2\sqrt{6}}+\sqrt{8-2\sqrt{15}}}{\sqrt{7+2\sqrt{10}}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

K

Kaijo

27 tháng 7 2020

1,Rút gọn biểu thức sau a,(\(\sqrt{3}-\sqrt{2}+1\) ).(\(\sqrt{3}-1\) ) b,(0,2\(\sqrt{\left(-10\right)^2.3}\) +2\(\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\) c,(\(\sqrt{28}-2\sqrt{14}+\sqrt{7}\) ).\(\sqrt{7}+7\sqrt{8}\) d,(\(15\sqrt{50}+5\sqrt{200}-3\sqrt{450}\)...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

2

NN

Nguyễn Ngọc Lộc

27 tháng 7 2020

a, \(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)-\sqrt{2}\left(\sqrt{3}-1\right)\)

\(=3-1-\sqrt{6}+\sqrt{2}=2+\sqrt{2}-\sqrt{6}\)

b, \(=\sqrt{300.0,04}+2\left|\sqrt{3}-\sqrt{5}\right|\)

\(=2\sqrt{3}+2\left(\sqrt{5}-\sqrt{3}\right)\)

\(=2\sqrt{3}+2\sqrt{5}-2\sqrt{3}=2\sqrt{5}\)

c, \(=\sqrt{196}-2\sqrt{98}+\sqrt{49}+7\sqrt{8}\)

\(=14-14\sqrt{2}+7+14\sqrt{2}=21\)

d, \(=15\sqrt{5}+5\sqrt{20}-3\sqrt{45}\)

\(=15\sqrt{5}+10\sqrt{5}-9\sqrt{5}=16\sqrt{5}\)

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

27 tháng 7 2020

Bài 1: Rút gọn

a) Ta có: \(\left(\sqrt{3}-\sqrt{2}+1\right)\cdot\left(\sqrt{3}-1\right)\)

\(=\left(\sqrt{3}+1\right)\cdot\left(\sqrt{3}-1\right)-\sqrt{2}\cdot\left(\sqrt{3}-1\right)\)

\(=3-1-\sqrt{6}+\sqrt{2}\)

\(=2-\sqrt{2}-\sqrt{6}\)

b) Ta có: \(0.2\cdot\sqrt{\left(-10\right)^2\cdot3}+2\cdot\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\)

\(=0.2\cdot\sqrt{\left(-10\right)^2}\cdot\sqrt{3}+2\cdot\left(\sqrt{5}-\sqrt{3}\right)\)

\(=0.2\cdot10\cdot\sqrt{3}+2\sqrt{5}-2\sqrt{3}\)

\(=2\sqrt{3}+2\sqrt{5}-2\sqrt{3}\)

\(=2\sqrt{5}\)

c) Ta có: \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\cdot\sqrt{7}+7\sqrt{8}\)

\(=\sqrt{196}-2\cdot\sqrt{98}+\sqrt{49}+7\sqrt{8}\)

\(=14-\sqrt{392}+7+\sqrt{392}\)

=21

d) Ta có: \(\left(15\sqrt{50}+5\sqrt{200}-3\sqrt{450}\right):\sqrt{10}\)

\(=15\sqrt{5}+5\sqrt{20}-3\sqrt{45}\)

\(=\sqrt{5}\left(15+5\cdot2-3\cdot3\right)\)

\(=16\sqrt{5}\)

Đúng(0)

HH

Hạ Hy

22 tháng 9 2019

rút gọn

a) \(\sqrt{\left(2-\sqrt{3}\right)^2}\) + \(\sqrt{4-2\sqrt{3}}\)

b) \(\sqrt{15-6\sqrt{5}}\) + \(\sqrt{33-12\sqrt{6}}\)

c) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)

#Hỏi cộng đồng OLM #Toán lớp 9

3

T

₮ØⱤ₴₮

22 tháng 9 2019

\(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}=\left|2-\sqrt{3}\right|+\sqrt{3-2\sqrt{3}+1}=2-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}=2-\sqrt{3}+\left|\sqrt{3}-1\right|=2-\sqrt{3}+\sqrt{3}-1=1\)

Đúng(0)

T

₮ØⱤ₴₮

22 tháng 9 2019

\((15\sqrt{200}-3\sqrt{450}+2\sqrt{50}):\sqrt{10}=\left(15.10\sqrt{2}-3.15\sqrt{2}+2.5\sqrt{2}\right):\sqrt{10}=\frac{115\sqrt{2}.1}{\sqrt{10}}=\frac{115\sqrt{20}}{10}\)

Đúng(0)

CD

Cỏ dại

9 tháng 6 2019 - olm

Rút gọn các biểu thức :

\(a,\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}}\)

\(b,\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

2

TD

Tớ Đông Đặc ATSM

9 tháng 6 2019

a,A.√2= √(4+2√3)-√(4-2√3)

= √(1+√3)² -√( √3 -1)²

= 1+√3-√3+1= 2

=> A= 2/√2=√2

Đúng(0)

TD

Tớ Đông Đặc ATSM

9 tháng 6 2019

B²= (4+√15)².(4-√15).(√10-√6)²

= (4+√15).1.(16-4√15)

= (4+√15).(4-√15).4

= 4

=> B = √4 = 2

Đúng(0)

TH

Thanh Hieu Nguyen

25 tháng 6 2018

A. RÚT GỌN:

a) \(\left(\sqrt{3}+2\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)

b) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)

Cầu cao nhân cứu em :(

#Hỏi cộng đồng OLM #Toán lớp 9

2

HH

Hắc Hường

25 tháng 6 2018

Giải:

a) \(\left(\sqrt{3}+2\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)

\(=\sqrt{3}.\sqrt{3}+2\sqrt{5}.\sqrt{3}-\sqrt{60}\)

\(=3+2\sqrt{15}-\sqrt{60}\)

\(=3+2\sqrt{15}-2\sqrt{15}\)

\(=3\)

Vậy ...

b) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)

\(=\left(15\sqrt{4.50}-3\sqrt{9.50}+2\sqrt{50}\right):\sqrt{10}\)

\(=\left(30\sqrt{50}-9\sqrt{50}+2\sqrt{50}\right):\sqrt{10}\)

\(=23\sqrt{50}:\sqrt{10}\)

\(=\dfrac{23\sqrt{50}}{\sqrt{10}}\)

\(=\dfrac{23\sqrt{5}\sqrt{10}}{\sqrt{10}}\)

\(=23\sqrt{5}\)

Vậy ...

Đúng(0)

TQ

Trần Quốc Lộc

25 tháng 6 2018

\(a\text{) }\left(\sqrt{3}+2\sqrt{5}\right)\sqrt{3}-\sqrt{60}\\ =3+2\sqrt{15}-2\sqrt{15}=3\)

\(b\text{) }\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\\ =15\sqrt{20}-3\sqrt{45}+2\sqrt{5}\\ =30\sqrt{5}-9\sqrt{5}+2\sqrt{5}\\ =\left(30-9+2\right)\sqrt{5}=23\sqrt{5}\)

Đúng(0)

KB

Không Biết

31 tháng 12 2019

1 rút gọn

\(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):10\)

2 k dùng máy tính hãy so sánh

\(\sqrt{3+\sqrt{20}}và\sqrt{5+\sqrt{5}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

2

AH

Akai Haruma

Giáo viên

1 tháng 1 2020

Bài 1:

\((15\sqrt{200}-3\sqrt{450}+2\sqrt{50}):10\)

\(=(15\sqrt{2.10^2}-3\sqrt{2.15^2}+2\sqrt{2.5^2}):10\)

\(=(15.10\sqrt{2}-3.15\sqrt{2}+2.5\sqrt{2}):10\)

\(=115\sqrt{2}:10=\frac{23\sqrt{2}}{2}\)

Đúng(0)

AH

Akai Haruma

Giáo viên

1 tháng 1 2020

Bài 2:

Ta có:

\(3+\sqrt{20}=3+\sqrt{2^2.5}=3+2\sqrt{5}=(3+\sqrt{5})+\sqrt{5}\)

\(>(3+\sqrt{4})+\sqrt{5}=(3+2)+\sqrt{5}=5+\sqrt{5}\)

\(\Rightarrow \sqrt{3+\sqrt{20}}> \sqrt{5+\sqrt{5}}\)

Đúng(0)

NC

Nhím Cute

7 tháng 8 2017 - olm

1 ) ( 15\(\sqrt{200}\) - 3\(\sqrt{450}\)+ 2\(\sqrt{50}\)) / \(\sqrt{10}\)2) Cho A = ( \(\frac{\sqrt{3}}{3+\sqrt{x}}\) + \(\frac{x+9}{9-x}\)) / ( \(\frac{3\sqrt{x}+1}{x-3\sqrt{x}}\) - \(\frac{1}{\sqrt{x}}\) )a/ Tìm điều kiện của x để A có nghĩab/ Rút gọn A c/ Tìm các giá trị của x để A <...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

0

KS

Km123 San Mine

22 tháng 4 2019 - olm

Rút gọn biểu thức

\(\sqrt{10+2\sqrt{6}+2\sqrt{10}+2\sqrt{15}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

DT

Đào Thu Hoà

23 tháng 4 2019

=\(\sqrt{\left(2+2\sqrt{6}+3\right)+\left(2\sqrt{10}+2\sqrt{15}\right)+5}\)

\(=\sqrt{\left[\left(\sqrt{2}\right)^2+2\sqrt{2}\sqrt{3}+\left(\sqrt{3}\right)^2\right]+\left(2\sqrt{2}\sqrt{5}+2\sqrt{3}\sqrt{5}\right)+\left(\sqrt{5}\right)^2}\)

\(=\sqrt{\left(\sqrt{2}+\sqrt{3}\right)^2+2\left(\sqrt{2}+\sqrt{3}\right)\sqrt{5}+\left(\sqrt{5}\right)^2}\)

\(=\sqrt{\left(\sqrt{2}+\sqrt{3}+\sqrt{5}\right)^2}=\sqrt{2}+\sqrt{3}+\sqrt{5}.\)

Đúng(0)

NC

Nhím Cute

7 tháng 8 2017 - olm

1 ) ( 15\(\sqrt{200}\) - 3\(\sqrt{450}\)+ 2\(\sqrt{50}\)) / \(\sqrt{10}\)2) Cho A = ( \(\frac{\sqrt{3}}{3+\sqrt{x}}\) + \(\frac{x+9}{9-x}\)) / ( \(\frac{3\sqrt{x}+1}{x-3\sqrt{x}}\) - \(\frac{1}{\sqrt{x}}\) )a/ Tìm điều kiện của x để A có nghĩab/ Rút gọn A c/ Tìm các giá trị của x để A < -1 #Giúp mình với...

Đọc tiếp