Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(=\left(\sqrt{ab}+\dfrac{2\sqrt{ab}}{a}-\sqrt{\dfrac{a^2+1}{ab}}\right)\cdot\sqrt{ab}\)
\(=ab+\dfrac{2ab}{a}-\sqrt{a^2+1}=ab+2b-\sqrt{a^2+1}\)
c: \(=2\sqrt{6b}-6\sqrt{18}+10\sqrt{12}-\sqrt{48}\)
\(=2\sqrt{6b}-18\sqrt{2}+20\sqrt{3}-4\sqrt{3}\)
\(=2\sqrt{6n}-18\sqrt{2}+16\sqrt{3}\)
d: \(=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\)

(bài 1) a) \(\dfrac{1}{5+2\sqrt{6}}-\dfrac{1}{5-2\sqrt{6}}\) = \(\dfrac{5-2\sqrt{6}-5-2\sqrt{6}}{25-24}\)
= \(\dfrac{-4\sqrt{6}}{1}\) = \(-4\sqrt{6}\)
b) \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\) = \(\sqrt{\left(\sqrt{5}+1\right)^2}-\dfrac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{3}}\)
= \(\left(\sqrt{5}+1\right)-\left(\sqrt{5}-1\right)\) = \(\sqrt{5}+1-\sqrt{5}+1\) = \(2\)
c) \(\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\) = \(\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\)
= \(\sqrt{6}.\sqrt{16}\) = \(4\sqrt{6}\)
d) \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\sqrt{3}+2+\sqrt{2}-\dfrac{1}{2-\sqrt{3}}\) = \(\dfrac{\left(\sqrt{3}+2+\sqrt{2}\right)\left(2-\sqrt{3}\right)-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{3}-3+4-2\sqrt{3}+2\sqrt{2}-\sqrt{6}-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{2}-\sqrt{6}}{2-\sqrt{3}}\) = \(\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{2}}\) = \(\sqrt{2}\)
e) \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\) = \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{1+\sqrt{5}}\)
= \(\dfrac{4}{1+\sqrt{3}}-\sqrt{3}\) = \(\dfrac{4-\sqrt{3}-3}{1+\sqrt{3}}\) = \(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
= \(\dfrac{\left(1-\sqrt{3}\right)\left(1-\sqrt{3}\right)}{1-3}\) = \(\dfrac{1-2\sqrt{3}+3}{-2}\) = \(\dfrac{4-2\sqrt{3}}{-2}\)
= \(\dfrac{-2\left(-2+\sqrt{3}\right)}{-2}\) = \(\sqrt{3}-2\)
bài 2)
a)\(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(a+b-2\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+a\sqrt{b}+b\sqrt{a}+b\sqrt{b}-2a\sqrt{b}-2b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+-a\sqrt{b}+b\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\) = \(\dfrac{a\left(\sqrt{a}-\sqrt{b}\right)-b\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\) = \(a-b\)
b) \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)^2-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(a-2\sqrt{a}+1\right)-\sqrt{a}\left(a+2\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{a\sqrt{a}-2a+\sqrt{a}-a\sqrt{a}-2a-\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2\left(a-1\right)}{4\sqrt{a}}.\dfrac{-4a}{a-1}\) = \(-2\)

Bài 3:
a: \(=\dfrac{3+2\sqrt{2}}{1}-\dfrac{\sqrt{2}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}\)
\(=3+2\sqrt{2}-\sqrt{2}=3+\sqrt{2}\)
b: \(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\left(\sqrt{ab}-b\right)}{\left(a+\sqrt{b}\right)^2}\)
\(=\dfrac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=\dfrac{b}{a+\sqrt{b}}\)
c: \(=x+\sqrt{x}-2\sqrt{x}-1+1=x-\sqrt{x}\)

câu g
(câu cuối) đề nhiều trôi hết nhìn thấy mỗi câu (g)
\(G=0,1\sqrt{200}+2\sqrt{0,08}+0,4\sqrt{50}\)
\(G=0,1.10\sqrt{2}+\dfrac{2.2}{10}\sqrt{2}+0,4.5\sqrt{2}\)
\(G=\sqrt{2}\left(1+\dfrac{2}{5}+2\right)=\dfrac{\sqrt{2}\left(5+2+10\right)}{5}=\dfrac{17\sqrt{2}}{5}\)

Câu 1 :
a ) \(\sqrt{0,36.100}=\sqrt{36}=6\)
b ) \(\sqrt[3]{-0,008}=\sqrt[3]{\left(-0,2\right)^3}=-0,2\)
c ) \(\sqrt{12}+6\sqrt{3}+\sqrt{27}=2\sqrt{3}+6\sqrt{3}+3\sqrt{3}=11\sqrt{3}\)
Câu 2 :
a ) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}=a-\sqrt{ab}+b\)

Bài 6:
a: \(\Leftrightarrow\sqrt{x^2+4}=\sqrt{12}\)
=>x^2+4=12
=>x^2=8
=>\(x=\pm2\sqrt{2}\)
b: \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>x+1=1
=>x=0
c: \(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}-20=0\)
=>\(\sqrt{2x}=2\)
=>2x=4
=>x=2
d: \(\Leftrightarrow2\left|x+2\right|=8\)
=>x+2=4 hoặcx+2=-4
=>x=-6 hoặc x=2

a, Vì trong dấu căn là số âm nên biểu thức này vô nghĩa. b)\(\sqrt{\dfrac{1}{200}}=\dfrac{1}{\sqrt{200}}=\dfrac{1}{10\sqrt{2}}=\dfrac{\sqrt{2}}{10\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{2}}{20}\)
c,\(\sqrt{\dfrac{7}{500}}=\dfrac{\sqrt{7}}{\sqrt{500}}=\dfrac{\sqrt{7}}{10\sqrt{5}}=\dfrac{\sqrt{7}.\sqrt{5}}{10\sqrt{5}.\sqrt{5}}=\dfrac{\sqrt{35}}{50}\)

ĐKXĐ : \(\left\{{}\begin{matrix}a,b\ge0\\a.b\ne1\end{matrix}\right.\)
a ) \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)+\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)-\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)-\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)+\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}.\dfrac{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}=-\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{2\left(\sqrt{a}+1\right)}=-\sqrt{ab}\)
Câu b : Ta có : \(b=\dfrac{\sqrt{3}-1}{1+\sqrt{3}}=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\dfrac{3-2\sqrt{3}+1}{2}=2-\sqrt{3}\)
\(P=-\sqrt{ab}=-\sqrt{\left(2-\sqrt{3}\right)^2}=-\left|2-\sqrt{3}\right|=\sqrt{3}-2\)
Câu c : \(\sqrt{a}+\sqrt{b}=4\Rightarrow\sqrt{a}=4-\sqrt{b}\)
\(P=-\sqrt{ab}=-\left(4-\sqrt{b}\right)\sqrt{b}=b-4\sqrt{b}=\left(\sqrt{b}-2\right)^2-4\ge-4\)
Vậy GTNN của P là -4 . Dấu bằng xảy ra khi \(a=b=4\)

a: \(=\dfrac{\sqrt{a}-1}{\sqrt{a}\left(a-\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{1}\)
\(=a-1\)
b: \(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}+\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{\sqrt{ab}+b+\sqrt{ab}-b}{\sqrt{a}\left(a-b\right)}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{1}{\sqrt{a}}\)
c: \(=\dfrac{a\sqrt{b}+b}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\cdot\left(\sqrt{a}+\sqrt{b}\right)\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(a+\sqrt{b}\right)^2}}\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=b\)

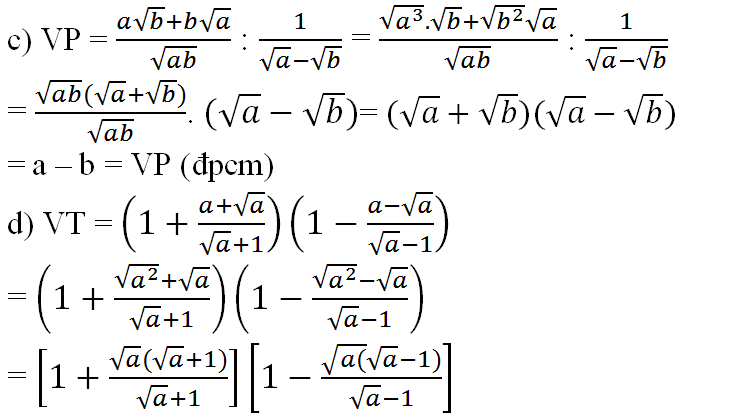
a: \(\dfrac{2}{\sqrt{3}-1}-\dfrac{2}{\sqrt{3}+1}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{3-1}\)
\(=\dfrac{2\sqrt{3}+2-2\sqrt{3}+2}{2}=\dfrac{4}{2}=2\)
b: \(\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}\)
\(=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}\)
\(=\dfrac{\sqrt{6}}{\sqrt{15}}=\sqrt{\dfrac{6}{15}}=\sqrt{\dfrac{2}{5}}=\dfrac{\sqrt{10}}{5}\)
c: \(\sqrt{9a}+\sqrt{81a}+3\sqrt{25a}-16\sqrt{49a}\)
\(=3\sqrt{a}+9\sqrt{a}+3\cdot5\sqrt{a}-16\cdot7\sqrt{a}\)
\(=27\sqrt{a}-112\sqrt{a}=-85\sqrt{a}\)
d: \(\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\sqrt{ab}-\sqrt{bc}}\)
\(=\sqrt{ab}+\sqrt{bc}\)
e: \(a\left(\sqrt{\dfrac{a}{b}+2\sqrt{ab}+b\cdot\sqrt{\dfrac{a}{b}}}\right)\cdot\sqrt{ab}\)
\(=a\cdot\sqrt{\dfrac{a}{b}\cdot ab+2\sqrt{ab}\cdot ab+b\cdot\sqrt{\dfrac{a}{b}}\cdot ab}\)
\(=a\cdot\sqrt{a^2+2\cdot ab\cdot\sqrt{ab}+a\sqrt{a}\cdot b\sqrt{b}}\)
\(=a\cdot\sqrt{a^2+3\cdot a\cdot\sqrt{a}\cdot b\cdot\sqrt{b}}\)
e: ĐKXĐ: a>=0 và a<>1
\(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}\)
\(=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\left(1+\sqrt{a}+\sqrt{a}+a\right)\cdot\left(a-\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\cdot\left(a-\sqrt{a}+1\right)\)