
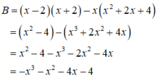
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

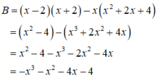

a, \(M=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\) (ĐK : \(\forall x\in R\))
\(=\sqrt{\left(x-2\right)^2}-\sqrt{\left(x+2\right)^2}\)
* Nếu x\(\ge2\Rightarrow M=x-2-x-2=-4\)
*Nếu x<2 => M=2-x-x-2=-2x
b,Để M=2\(\ne-4\)
=>M=-2x
=>-2x=-4
=>x=2
__________________________________________________________________________________________
P=\(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
* Nếu \(x\ge2\Rightarrow P=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
* Nếu x<2 =>P=\(\sqrt{x-1}+1+1-\sqrt{x-1}=2\)
VẬY.......
Tk nha!

\(B=\frac{x^2}{x-2}.\left(\frac{x^2+4}{x}-4\right)-x^2\)
\(B=\frac{-2x^3+4x^2}{x^2-2x}\)
\(B=\frac{-2x^2+4x}{x-2}\)
\(B=\frac{2x\left(-x+2\right)}{x-2}\)
\(B=-2x\)

\(E=\frac{x^2}{x-2}.\left(\frac{x^2+4}{x}-4\right)+3\)( \(ĐK:x\ne2;x\ne0\))
\(=\frac{x^2}{x-2}.\frac{x^2-4x+4}{x}+3\)
\(=\frac{x^2}{x-2}.\frac{\left(x-2\right)^2}{x}+3=x\left(x-2\right)+3=x^2-2x+3\)
b, \(E=x^2-2x+3=\left(x-1\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi \(x-1=0\Rightarrow x=1\)
Vậy GTNN của E là 2 khi x = 1

a/
\(A=\frac{3}{x+2}-\frac{2}{2-x}-\frac{8}{x^2-4}\)
\(=\frac{3}{x+2}+\frac{2}{x-2}-\frac{8}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{3x-6+2x+4-8}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{5x-10}{\left(x+2\right)\left(x-2\right)}=\frac{5}{x+2}\)
b/ Thay x = 3 thì ta được
\(\frac{5}{3+2}=1\)

a)\(\frac{x^3-x}{3x+3}=\frac{x.\left(x^2-1\right)}{3.\left(x+1\right)}=\frac{x.\left(x-1\right).\left(x+1\right)}{3.\left(x+1\right)}=\frac{x.\left(x+1\right)}{3}=\frac{x^2+x}{3}\)

Bạn rút gọn sai rồi, mình nhìn đề bài b) cho x>2 thì là biết chắc bạn sai , mình làm lại nhé : ( ĐKXĐ : tự làm )
a) \(Q=\frac{x\left(x+2\right)}{\left(x-2\right)^2}:\left(\frac{\left(x+2\right)\left(x-2\right)+x+6-x^2}{x\left(x-2\right)}\right)\)
\(=\frac{x\left(x+2\right)}{\left(x-2\right)^2}:\frac{x+2}{x\left(x-2\right)}\)
\(=\frac{x\left(x+2\right)}{\left(x-2\right)^2}\cdot\frac{x\left(x-2\right)}{x+2}=\frac{x^2}{x-2}\)
Vậy \(Q=\frac{x^2}{x-2}\)
b) Ta có : \(Q=\frac{x^2}{x-2}=\frac{x^2-4+4}{x-2}=x+2+\frac{4}{x-2}=x-2+\frac{4}{x-2}+4\)
Do \(x>2\Rightarrow x-2>0\) và \(\frac{4}{x-2}>0\)do đó áp dụng BĐT Cô si cho 2 số dương ta được :
\(x-2+\frac{4}{x-2}\ge2\sqrt{\left(x-2\right).\left(\frac{4}{x-2}\right)}=2\cdot\frac{1}{2}=1\)
\(\Rightarrow Q\ge1+4=5\)
Vậy : GTNN của \(Q=5\)
P/s : Ai vào kiểm tra hộ cái :)) Sợ sai lắm nhé, cảm ơn nha 33
Nếu chưa học Cô si thì chứng minh rồi dùng thôi :
Bài này sử dụng Cô - si hai số nên cần chứng minh BĐT :
\(a+b\ge2\sqrt{ab}\left(a,b>0\right)\)
Thật vậy : \(a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) ( luôn đúng )
Do đó \(a+b\ge2\sqrt{ab}\) với a,b >0
Dấu "=" xảy ra \(\Leftrightarrow a=b\)

ĐK: x khác +-2
\(C=\left(\frac{2}{x+2}-\frac{x}{\left(x-2\right)\left(x+2\right)}+\frac{1}{x-2}\right).\left(\frac{x-2}{x^2-4+6-x^2}\right)\\ \)
\(C=\frac{2\left(x-2\right)-x+\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}.\left(\frac{x-2}{2}\right)=\frac{2\left(x-1\right)\left(x-2\right)}{2.\left(x-2\right)\left(x+2\right)}\)
\(C=\frac{x-1}{x+2}\)
C=[2/(x+2)-x/(x^2-4)-1/(2-x)]:[x+2+(6-x^2)/(x-2)]
=[2/(x+2)-x/(x-2)(x+2)-(-1)/(x-2)]:[x+2+(6-x^2)/(x-2)]
=[2x-4-x+x+2/(x-2)(x+2)]:[(x^2-4+6-x^2)/(x-2)]
=2x-2/(x-2)(x+2) . (x-2)/2
=2(x-1)/(x-2)(x+2) . (x-2)/2
=x-1/x+2

\(A=\frac{x-1}{x+2}-\frac{x+2}{x-2}-\frac{x^2+12}{4-x^2}\) ĐKXĐ: \(x\ne\pm2\)
\(=\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\frac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}+\frac{x^2+12}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x^2-2x-x+2-x^2-4x-4+x^2+12}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x^2-7x+10}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x^2-2x-5x+10}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x\left(x-2\right)-5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{\left(x-5\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x-5}{x+2}\)