HA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
12 tháng 7 2023
\(A=\sqrt{x}+1\) (đã thu gọn)
\(B=\dfrac{4\sqrt{x}}{x+4}\) (đã thu gọn)
\(A=x-\sqrt{x}+1=\sqrt{x}\cdot\sqrt{x}-\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}-1\right)+1\)
\(A=\dfrac{3}{2\sqrt{x}}\) (đã thu gọn)
\(A=\dfrac{3}{\sqrt{x}+3}\) (đã thu gọn)
\(A=1-\sqrt{x}\) (đã thu gọn)
\(A=x-2\sqrt{x}-1=\sqrt{x}\left(\sqrt{x}-2\right)-1\)
LL
2 tháng 7 2023
`a)->` ĐKXĐ : `x>=0;x\ne1`
`b)` Ta có :
`P=(\sqrtx)/(\sqrtx-1)-(2\sqrtx)/(\sqrtx+1)+(x-3)/(x-1)`
`P=(\sqrtx(\sqrtx+1)-2\sqrtx(\sqrtx-1)+x-3)/(x-1)`
`P=(x+\sqrtx-2x+2\sqrtx+x-3)/(x-1)`
`P=(3\sqrtx-3)/(x-1)`
`P=(3(\sqrtx-1))/((\sqrtx-1)(\sqrtx+1))`
`P=3/(\sqrtx+1)`
Vậy `P=3/(\sqrtx+1)` khi `x>=0;x\ne1`
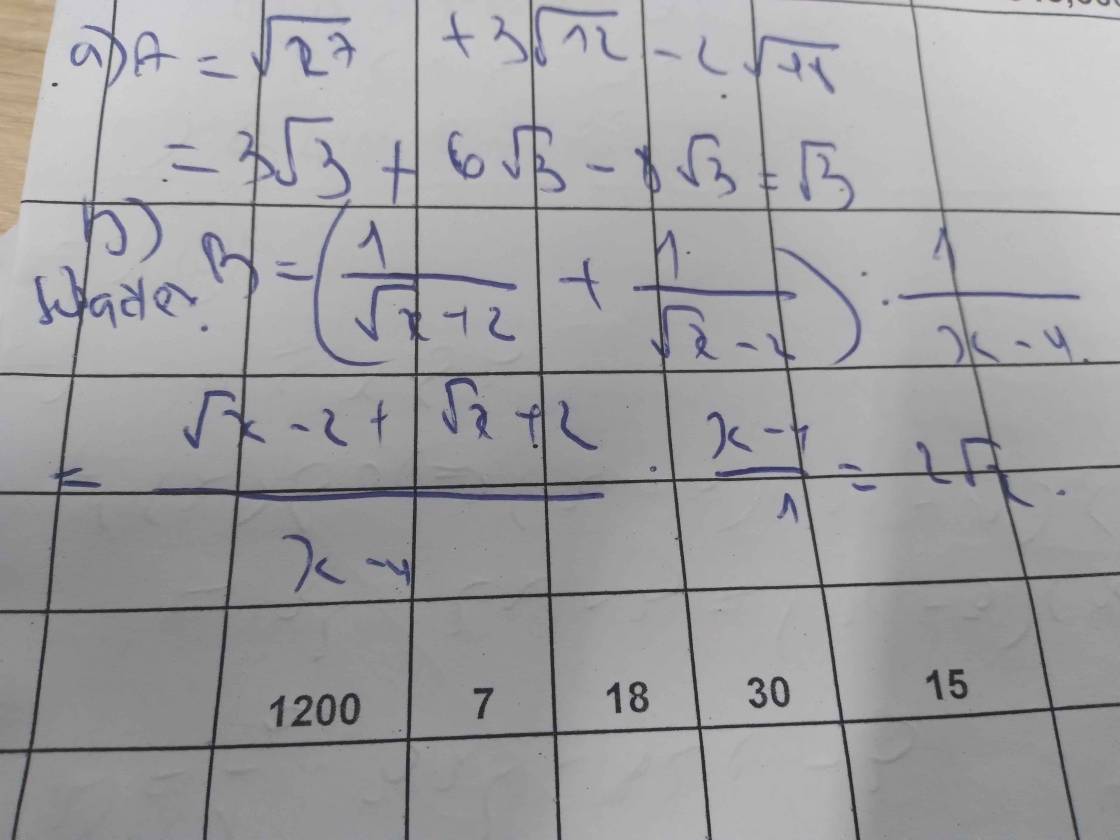
Ta có: \(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{4\sqrt{x}+12}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{8\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{8}{\sqrt{x}-3}\)