Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^{n-1}.\left(x^2-1\right)-x\left(x^{n-1}-x^{n-2}\right)\)
\(\Rightarrow x^{n-1+2}-x^{n-1}-x^{n-1+1}+x^{n-2+1}\)
\(\Rightarrow x^{n+1}-x^{n-1}-x^n+x^{n-1}\)
\(\Rightarrow x^{n+1}-x^n\)

a)ko bít đề bắt làm j
b)Px=x(1+x+x2+...+x2015+x2018)
Px=x+x2+...+x2017
Px-P=(x+x2+...+x2017)-(1+x+x2+...+x2015+x2018)
P(x-1)=x2017-1
P=(x2017-1)/(x-1)

1: \(\dfrac{A}{B}=\dfrac{4}{3}x^{n+1-3}y^{2-n+1}=\dfrac{4}{3}x^{n-2}y^{3-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-2>=0\\3-n< =0\end{matrix}\right.\Leftrightarrow2< =n< =3\)
2: \(\dfrac{A}{B}=\dfrac{7}{5}x^{n-1-2}y^{5-n}-xy^{4-n}=\dfrac{7}{5}x^{n-3}y^{5-n}-xy^{4-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-3>=0\\5-n>=0\\4-n>=0\end{matrix}\right.\Leftrightarrow3\le n\le4\)
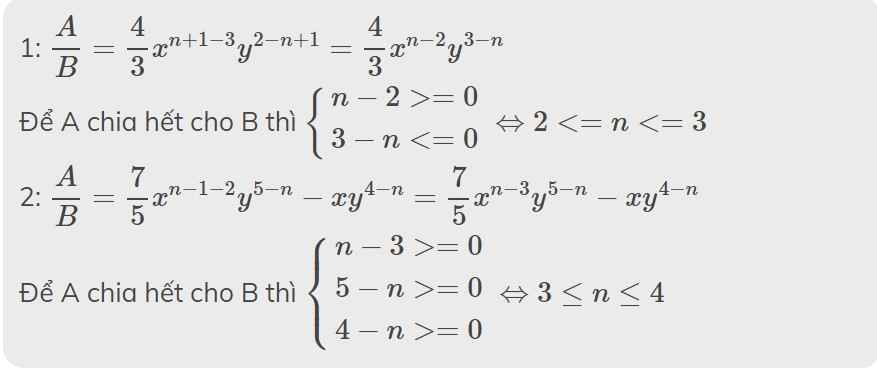
\(3x^{n-2}.\left(x^{n+2}-y^{n+2}\right)+y^{n+2}.\left(3x^{n-2}-y^{n-5}\right)\)
\(=3x^{n-2}.x^{n+2}-3x^{n-2}.y^{n+2}+y^{n+2}.3x^{n-2}-y^{n+2}.y^{n-5}\)
\(=3x^{2n}-\left(3xy\right)^{n-2}.y^4+\left(3xy\right)^{n-2}.y^4-y^{2n-3}\)
\(=3x^{2n}-y^{2n-3}\)
Chúc bạn học tốt!!!
\(\text{Ta có : }\)
\(\\ 3x^{n-2}\left(x^{n+2}-y^{n+2}\right)+y^{n+2}\left(3x^{n-2}-y^{n-5}\right)\)
\(\\ =3x^{n-2}\cdot x^{n+2}-3x^{n-2}\cdot y^{n+2}+y^{n+2}\cdot3x^{n-2}-y^{n+2}\cdot y^{n-5}\)
\(\\ =3x^{\left(n+2\right)+\left(n-2\right)}+\left(-3x^{n-2}\cdot y^{n+2}+y^{n+2}\cdot3x^{n-2}\right)-y^{\left(n+2\right)+\left(n-5\right)}\)
\(=3x^{n+2+n-2}-y^{n+2+n-5}\)
\(=3x^{\left(n+n\right)+\left(2-2\right)}-y^{\left(n+n\right)+\left(2-5\right)}\)
\(=3x^{2n}-y^{2n-3}\)