Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

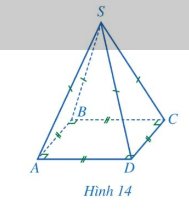
Hình chóp tứ giác đều S.ABCD có:
- Mặt đáy ABCD là hình vuông.
- Các mặt bên là SAB, SBC, SCD, SDA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CD, DA bằng nhau.
- Các cạnh bên SA, SB, SC, SD bằng nhau.
- S gọi là đỉnh của hình chóp đều S. ABCD

| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |

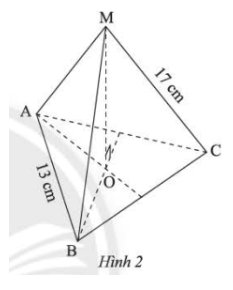
a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)

Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

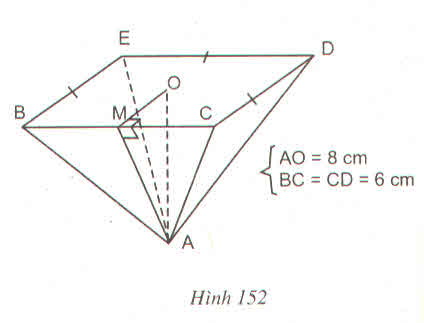
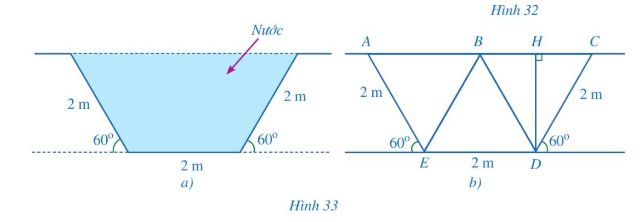
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)

Các miếng bìa ở hình 9a có thể gấp lại thành hình chóp tam giác đều.
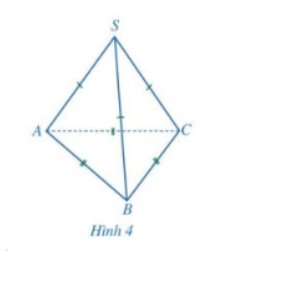


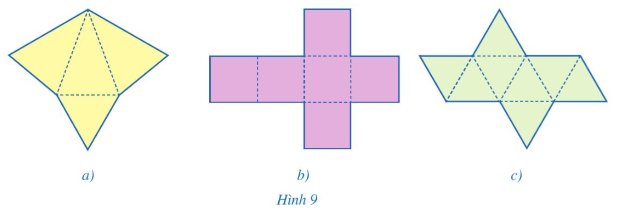
Hình chóp tam giác đều S. ABCD có:
- Mặt đáy: ABC là một tam giác đều
- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.
- Các cạnh đáy: AB, BC, CA bằng nhau.
- Các cạnh bên; SA, SB, SC, SD
- S gọi là đỉnh của hình chóp tam giác đều S. ABC