Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

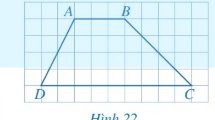
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

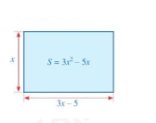
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

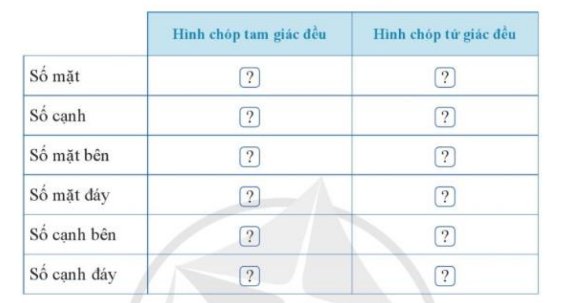
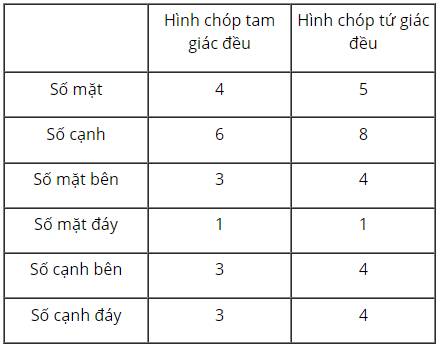
Những hình khối có dạng ở hình 11 được gọi là hình chóp tứ giác đều.

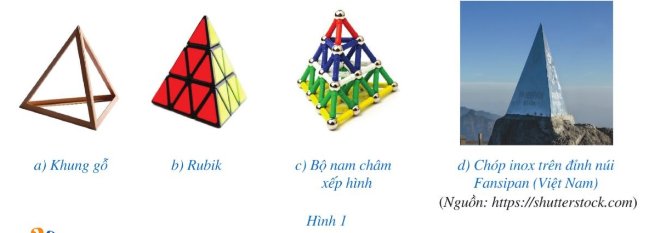
Những hình khối có dạng như ở Hình 1 thường được gọi là hình chóp tam giác đều.

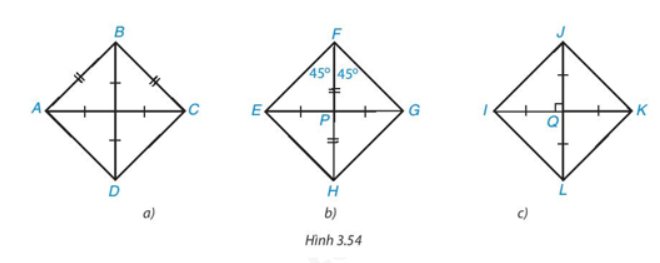
• Hình 3.54a)
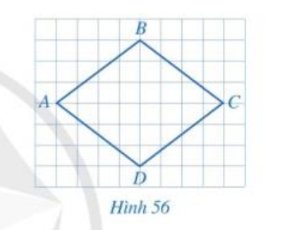
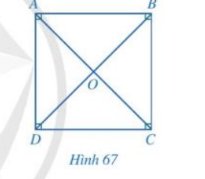
Tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác này là hình chữ nhật.
Mà AB = BC nên tứ giác ABCD là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình 3.54b)
Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm P của mỗi đường.
Ta có \[\widehat {EFG} = \widehat {EFP} + \widehat {GFP} = {45^o} + {45^o} = {90^o}\]
Suy ra tứ giác EFGH là hình chữ nhật.
Hình chữ nhật EFGH có đường chéo FH là đường phân giác của \(\widehat {EFG}\).
Do đó tứ giác EFGH là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.
• Hình 3.54c)
Tứ giác IJKL có hai đường chéo IK và JL bằng nhau và cắt nhau tại trung điểm Q của mỗi đường.
Suy ra tứ giác IJKL là hình chữ nhật.
Mà IK ⊥ JL nên tứ giác IJKL là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình vuông

Do tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)
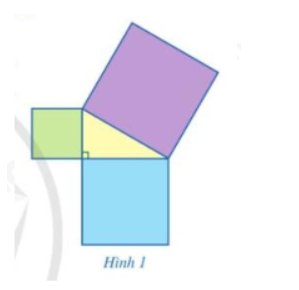


Bạn Đan đã dựa vào định lí Py-ta-go (tổng bình phương hai cạnh góc vuông bằng bình phương cạnh huyền) để chứng minh khẳng định trên.