Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

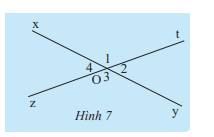
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

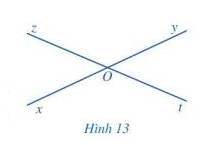
a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.

Bài 1:
x O n t m y
a)
Ta có: góc xOt + góc yOt = 180 độ ( kề bù )
Mà góc yOt = 60 độ ( gt )
=> góc xOt = 180 độ - 60 độ = 120 độ
b)
On là phân giác góc xOt ( gt ) => góc xOn = \(\frac{1}{2}\)góc xOt = \(\frac{1}{2}\). 120 độ = 60 độ
On là phân giác góc yOt ( gt ) => góc mOt = \(\frac{1}{2}\)góc yOt = \(\frac{1}{2}\). 60 độ = 30 độ
=> góc xOn + góc mOt = 60 độ + 30 độ = 90 độ
=> góc xOn và góc mOt là hai góc phụ nhau
Bài 2:
O x' y z x
b)
Cặp góc kề bù: góc x'Oz và góc zOy
O x n t m y
a,ta có : xot+yot=xoy
mà xoy=180o ; yot=60o (gt)
=> xot+60=180
=>. xot =180-60
=> xot=120o
b, Vì om là phân giác của góc yot. (gt)
=> yom=mot=yot/2
Vì on là phân giác của góc xot .(gt)
=> xon=not=xot/2
ta có : not+mot=xot/2+yot/2
hay not+mot=xot+yot/2
=> not+yot=180/2=90o
Vậy not và yot là hai góc phụ nhau.

Trả lời :
Bn tham khảo đường link này nhé ^^
Câu hỏi của khongcanten - Toán lớp 7 - Học toán với OnlineMath
Chúc bn hc tốt <3
x O y z t
Ta có : \(\widehat{xOt}\)và \(\widehat{xOz}\)là 2 góc kề bù nên \(\widehat{xOt}+\widehat{xOz}=180^o\)( tc góc kề bù )
mà \(\widehat{xOt}=4\widehat{xOz}\)
Do đó \(4\widehat{xOt}+\widehat{xOz}=180^o\)hay \(5\widehat{xOz}=180^o\)
Vậy \(\widehat{xOz}=180^o:5=36^o\)
Suy ra \(\widehat{xOt}=4.36^o=144^o\)
Các cặp góc \(\widehat{yOz}\)và \(\widehat{xOt}\), \(\widehat{tOy}\)và \(\widehat{xOz}\)là các cặp góc đổi đỉnh do đó:
\(\widehat{yOz}=\widehat{xOt}=144^o\)
\(\widehat{tOy}=\widehat{xOz}=36^o\)
Chúc bạn học tốt !!!

Bài 2:
x O y z m n
Ta có:
\(\widehat{xOz}+\widehat{yOz}=180^o\) (hai góc kề bù) (1)
mà Om và On là phân giác của \(\widehat{xOz};\widehat{yOz}\).
\(\Rightarrow\widehat{mOz}=\dfrac{\widehat{xOz}}{2};\widehat{nOz}=\dfrac{\widehat{yOz}}{2}\)(2)
Từ (1) và (2) suy ra:
\(\dfrac{\widehat{xOz}}{2}+\dfrac{\widehat{yOz}}{2}=\dfrac{180^o}{2}\)
\(\Rightarrow\widehat{mOz}+\widehat{nOz}=90^o\)
\(\Rightarrow\widehat{mOn}=90^o\)
Vậy góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông (đpcm)
Chúc bạn học tốt!!
x y z t O
Ta có :
\(xOy=180^0\)
\(xOy=2yOt\)
\(\Rightarrow yOt=90^0\)
\(xOt+yOt=180^0\)
\(\Rightarrow xOt=90^0\)
\(xOz+xOt=180^0\)
\(\Rightarrow xOz=90^0\)
Vậy :\(xOy=180^0\)
\(yOt=90^0\)
\(xOt=90^0\)
\(xOz=90^0\)
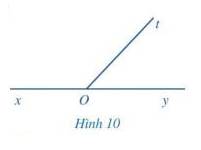
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng