Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

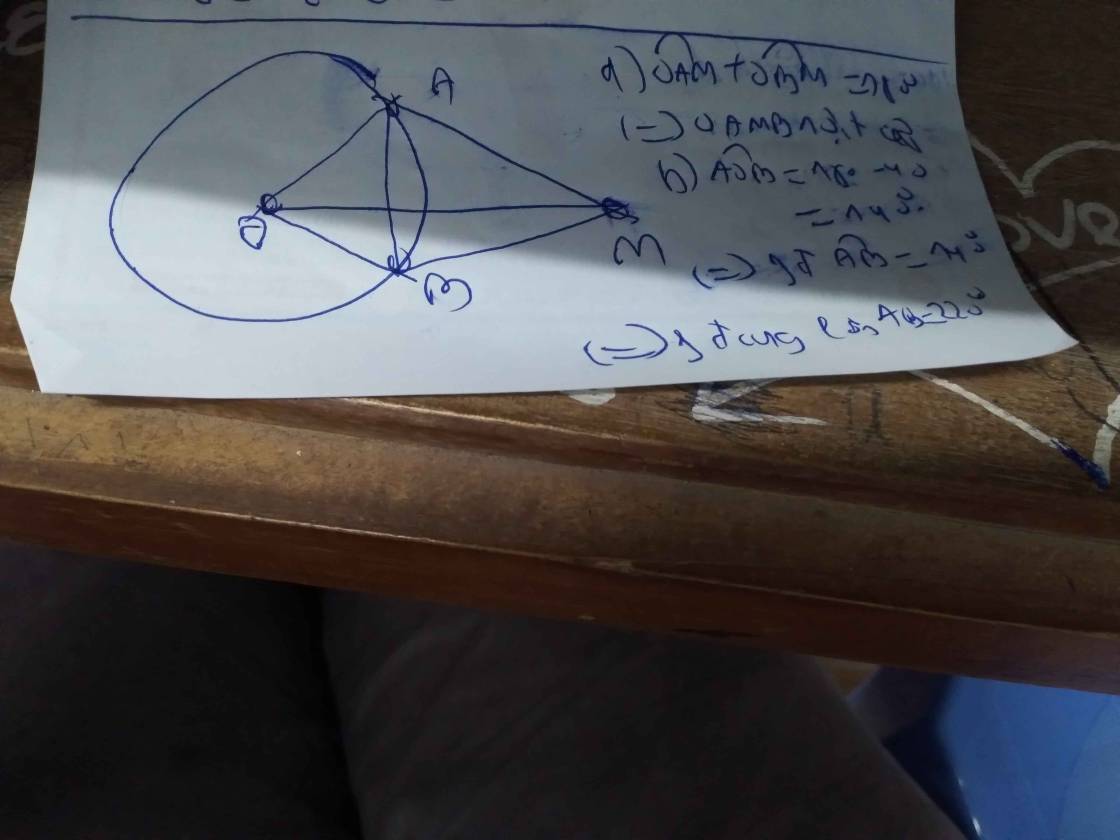
a: Xét (O) có
\(\widehat{AMC}\) là có đỉnh ở bên ngoài đường tròn chắn hai cung AC và BD
=>\(\widehat{AMC}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BD}-sđ\stackrel\frown{AC}\right)=\dfrac{1}{2}\left(180^0-60^0\right)=60^0\)
Xét (O) có
ΔBAD nội tiếp
BD là đường kính
Do đó: ΔBAD vuông tại A
=>DA\(\perp\)MB tại A
Xét (O) có
ΔCBD nội tiếp
BD là đường kính
Do đó: ΔCBD vuông tại C
=>BC\(\perp\)MD tại C
Xét tứ giác MAIC có \(\widehat{MAI}+\widehat{MCI}+\widehat{AMC}+\widehat{AIC}=360^0\)
=>\(\widehat{AIC}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AIC}=120^0\)
b: Xét ΔMCB vuông tại C và ΔMAD vuông tại A có
\(\widehat{M}\) chung
Do đó: ΔMCB~ΔMAD
=>\(\dfrac{MC}{MA}=\dfrac{MB}{MD}\)
=>\(MA\cdot MB=MC\cdot MD\)

Xét ΔODB có OD=OB(gt)
nên ΔODB cân tại O(Định nghĩa tam giác cân)
Xét ΔOBD cân tại O có \(\widehat{DOB}=60^0\left(sđ\stackrel\frown{BD}=60^0\right)\)
nên ΔOBD đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{OBD}=60^0\)(Số đo của một góc trong ΔOBD đều)
\(\Leftrightarrow\widehat{ABM}=60^0\)
Ta có: ΔBAM vuông tại A(gt)
nên \(\widehat{ABM}+\widehat{AMB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{AMB}+60^0=90^0\)
hay \(\widehat{AMB}=30^0\)
Vậy: \(\widehat{AMB}=30^0\)

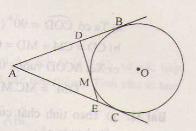
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
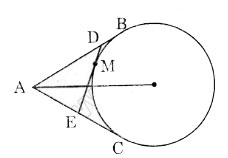
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB