Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kiến thức áp dụng
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.


⇒ A ^ + B S M ^
= 1 2 . s đ N C ⏜ - s đ B M ⏜ + 1 2 s đ N C ⏜ + s đ M B ⏜ = s đ N C ⏜ 1
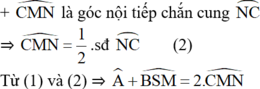
(đpcm)

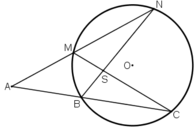
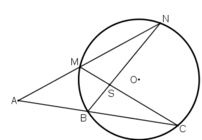
Điểm A nằm ngoài đường tròn (O) kẻ tiếp tuyến ABC vầ AMN, BN cắt CM tại S
Cmr
a, ^A+^BSM=2^CBN
b, AM. AN= AB.AC

a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI ⊥⊥ MN, OK ⊥⊥ PQ.
Trong đường tròn nhỏ, ta có: MN > PQ ⇒⇒ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK ⇒⇒ AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d) OI<OK⇒OIOA<OKOAOI<OK⇒OIOA<OKOA
⇒sinˆOAI<sinˆOAK⇒ˆOAI<ˆOAK⇒ˆOAE<ˆOAH.
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI \bot⊥ MN, OK \bot⊥ PQ.
Trong đường tròn nhỏ, ta có: MN > PQ \Rightarrow⇒ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK \Rightarrow⇒ AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d) OI < OK\Rightarrow\frac{OI}{OA}<\frac{OK}{OA}OI<OK⇒OAOI<OAOK
\Rightarrow \sin{\widehat{OAI}}< \sin{\widehat{OAK}} \Rightarrow \widehat{OAI}<\widehat{OAK} \Rightarrow \widehat{OAE}<\widehat{OAH}.⇒sinOAI<sinOAK ⇒OAI<OAK⇒OAE<OAH.
nè