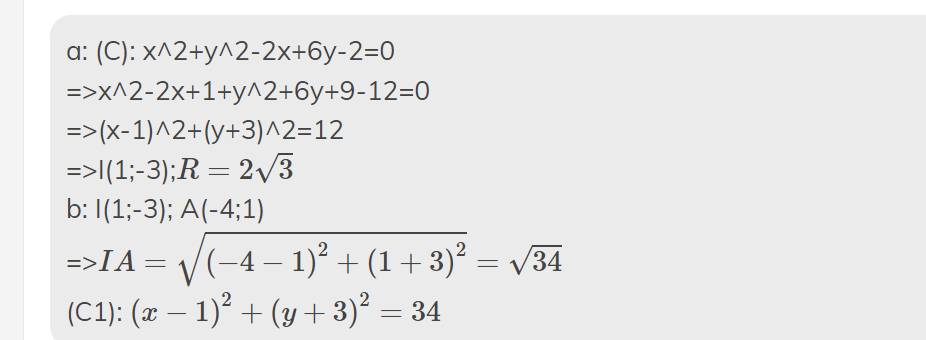Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tâm I(2 ; -4), R = 5
b) Đường tròn có phương trình: (x – 2 )2 + (y + 4)2 = 25
Thế tọa độ A(-1 ; 0) vào vế trái, ta có :
(-1- 2 )2 + (0 + 4)2 = 32 + 42 = 25
Vậy A(-1 ;0) là điểm thuộc đường tròn.
Áp dụng công thức tiếp tuyến (Xem sgk)
Ta được pt tiếp tuyến với đường tròn tai A là:
(-1 – 2)(x – 2) + (0 + 4)(y + 4) = 25 <=> 3x – 4y + 3 = 0
Chú ý:
1. Theo tính chất tiếp tuyến với đường tròn tại 1 điểm thuộc đường tròn thì vuông góc với bán kính đi qua tiếp điểm, ta có thể giải câu này như sau:
Vectơ = (-3; 4)
Tiếp tuyến đi qua A(-1; 0) và nhận làm một vectơ pháp tuyến có phương trình:
-3(x + 1) + 4(y – 0) = 0 ,<=> 3x – 4y + 3 = 0

Bài 1:
\(2c=8\Rightarrow c=4\)
Gọi phương trình (E) có dạng \(\frac{x^2}{a^2}+\frac{y^2}{a^2-16}=1\)
Do A thuộc (E) nên \(\frac{0}{a^2}+\frac{9}{a^2-16}=1\Rightarrow a^2=25\)
Phương trình (E): \(\frac{x^2}{25}+\frac{y^2}{9}=1\)
Bài 2:
\(2a=10\Rightarrow a=5\)
\(e=\frac{c}{a}\Rightarrow c=e.a=\frac{3}{5}.5=3\)
Phương trình elip:
\(\frac{x^2}{25}+\frac{y^2}{16}=1\)
Câu 3:
\(x-2y+3=0\Rightarrow x=2y-3\)
Thay vào pt đường tròn ta được:
\(\left(2y-3\right)^2+y^2-2\left(2y-3\right)-4y=0\)
\(\Leftrightarrow5y^2-20y+15=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-1\\y=3\Rightarrow x=3\end{matrix}\right.\)
Tọa độ 2 giao điểm: \(A\left(-1;1\right)\) và \(B\left(3;3\right)\)
Câu 4:
Gọi d' là đường thẳng song song với d \(\Rightarrow\) pt d' có dạng \(x-y+c=0\)
Do d' tiếp xúc với (C) nên \(d\left(I;d'\right)=R\)
\(\Rightarrow\frac{\left|0.1-0.1+c\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\Rightarrow\left|c\right|=2\Rightarrow c=\pm2\)
Có 2 pt đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x-y+2=0\\x-y-2=0\end{matrix}\right.\)

Sửa đề: (C) \(x^2+y^2+2x-4y=0\)
Đường tròn tâm \(I\left(-1;2\right)\) bán kính \(R=\sqrt{5}\)
Do MA; MB là tiếp tuyến \(\Rightarrow MA=MB\)
Mà \(\widehat{AMB}=60^0\Rightarrow\Delta AMB\) đều \(\Rightarrow MA=MB=AB\)
\(\widehat{AIB}=180^0-60^0=120^0\)
\(\Rightarrow AB=\sqrt{IA^2+IB^2-2IA.IB.cos120^0}=\sqrt{15}\)
\(\Rightarrow IM=\sqrt{IA^2+AM^2}=\sqrt{5+15}=2\sqrt{5}\)
Do \(M\in d\Rightarrow M\left(m;m+1\right)\) \(\Rightarrow\overrightarrow{IM}=\left(m+1;m-1\right)\)
\(\Rightarrow\left(m+1\right)^2+\left(m-1\right)^2=20\)
\(\Leftrightarrow2m^2+2=20\Rightarrow m^2=9\Rightarrow\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(3;4\right)\\M\left(-3;-2\right)\end{matrix}\right.\)

\(x-7y+10=0\Rightarrow x=7y-10\)
Thay vào pt đường tròn:
\(\left(7y-10\right)^2+y^2-2\left(7y-10\right)+4y-20=0\)
\(\Leftrightarrow y^2-3y+2=0\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-3\\y=2\Rightarrow x=4\end{matrix}\right.\)
Gọi \(B\left(-3;1\right);C\left(4;2\right)\)
Phương trình trung trực AB có dạng:
\(4\left(x+1\right)-3\left(y+\frac{1}{2}\right)=0\Leftrightarrow8x-6y+5=0\)
Phương trình trung trực BC có dạng:
\(7\left(x-\frac{1}{2}\right)+1\left(y-\frac{3}{2}\right)=0\Leftrightarrow7x+y-5=0\)
Tọa độ tâm I là nghiệm: \(\left\{{}\begin{matrix}8x-6y+5=0\\7x+y-5=0\end{matrix}\right.\) \(\Rightarrow I\left(\frac{1}{2};\frac{3}{2}\right)\)
\(\Rightarrow R^2=IA^2=\sqrt{\left(1-\frac{1}{2}\right)^2+\left(-2-\frac{3}{2}\right)^2}=\frac{25}{2}\)
Phương trình: \(\left(x-\frac{1}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=\frac{25}{2}\)
Quy trình làm như vậy, còn các bước tính toán bạn kiểm tra lại

a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$