Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cần tìm là abcdef
a có 4 cách chọn
+ với a = { 1,2,3}
b có 5 cách chọn
c có 4 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\) có 360 số
+ với a = 4
b có 3 cách chọn
b={ 1,2}
c có 4 cách chọn
d có́ 3 cách chọn
e có 2 cách choṇ
f có 1 cách chọn
b =3
c có 1 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\)có 54 số
vậy có 360 + 54 = 414 số

Gọi số cần lập là \(\overline{abcd}\)
TH1: \(a=1\)
\(\Rightarrow\) Bộ bcd có \(A_6^3=120\) số
TH2: \(a=2\Rightarrow b=0\) \(\Rightarrow c=1\)
d có 4 cách chọn \(\Rightarrow4\) số
\(\Rightarrow120+4=124\) số

Gọi số tự nhiên cần tìm có dạng \(\overline{abcde}\)
Do a chỉ thuộc {1;2} nên ta chia 2 trường hợp
Trường hợp a=2(b<5):
b có 5 cách chọn
c có 5 cách chọn
d có 4 cách chọn
e có 3 cách chọn
Do đó với trường hợp a=2 ta có: 5.5.4.3=300(cách)
Trường hợp a=1:
b có 6 cách chọn
c có 5 cách chọn
d có 4 cách chọn
e có 3 cách chọn
Do đó trường hợp a=1 có 6.5.4.3=360(cách)
Từ đó để lập được các số tự nhiên thõa đề có: 300+360=660(cách)
Bạn có thể kiểm tra kỹ lại, trong quá trình làm có thể có sai xót về số nhưng hướng làm thì ổn rồi

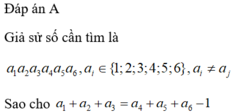
![]()
![]()
![]()
![]()
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: ![]()

TH1: Số cần lập có dạng \(520\overline{ab}\)
Chọn a;b có \(A^2_4\) cách
TH2 : Số cần lập có dạng : \(50\overline{abc}\)
Chọn a;b;c có \(A^3_5\) cách
TH3: Số cần lập có dạng : \(\overline{abcde}\left(a\ne5\right)\)
Chọn a: 2 cách
Chọn b;c;d;e có \(A^4_6\) cách
Vậy lập được tất cả \(A^2_4+A^3_5+2A^4_6=792\) số

Ta có 1+2+3+4+5+6+ =21 Vậy tổng của 3 chữ số đầu là 10
Dễ thấy 1+3+6 = 1+4+5 = 2+3+5
Vậy có 3 cách chọn 3 nhóm 3 chữ số đầu (1,3,6 hoặc 1,4,5 hoặc 2,3,5)
Với 1 cách chọn nhóm 3 chữ số thì có 3! cách để lập ra số \(\overline{a_1a_2a_3}\)
Với 3 số còn lại thì có 3! cách để lập ra số \(\overline{a_4a_5a_6}\)
(ở đây \(\overline{a_1a_2a_3a_4a_5a_6}\) là số thỏa mãn yêu cầu đề ra)
Theo quy tắc nhân ta có 3.6.6 = 108
Vậy có 108 số cần tìm
Em thấy như này còn thiều trường hợp hay sao ý ạ tại ba số nhỏ hơn đâu nhất thiết phải bằng 10 ạ 123 vs 345 vẫn tỏa mãn đấy chứ ạ.Có thể cho em là mình sai ở đâu hay kế quả thế nào được không ạ??

Gọi các số cần tìm có dạng tổng quát là abc
Dựa vào các chữ số, lập được:
a có 3 cách chọn chữ số hàng trăm vì 0<a<5 => a= {1;2;3}
b có 8 cách chọn chữ số hàng chục - tất cả các số trên đều có đủ điều kiện để là c/s hàng chục
c có 8 cách chọn chữ số hàng đơn vị - tất cả các số trên đều có đủ điều kiện để là c/s hàng đơn vị
Bạn lập như thế với các số có dạng 5ab với a<2 và b<6 nhé!
=> Lập được các số để thỏa mãn ycđb là: 3x8x8+?= ? số
_HT_