Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

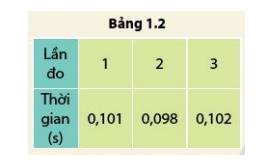
Thời gian trung bình của phép đo là:
\(\overline t = \frac{{{t_1} + {t_2} + {t_3}}}{3} = \frac{{0,101 + 0,098 + 0,102}}{3} \approx 0,100(s)\)
Sai số tuyệt đối trung bình của phép đo là:
\(\begin{array}{l}\Delta {t_1} = \left| {{t_2} - {t_1}} \right| = \left| {0,098 - 0,101} \right| = 0,003\\\Delta {t_2} = \left| {{t_3} - {t_2}} \right| = \left| {0,102 - 0,098} \right| = 0,004\\\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2}}}{2} = \frac{{0,003 + 0,004}}{2} \approx 0,004(s)\end{array}\)

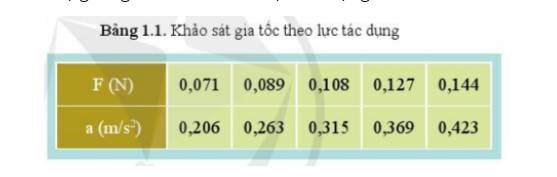
Mối liên hệ giữa gia tốc của xe với lực tác dụng lên nó là:
Gia tốc tỉ lệ thuận với lực tác dụng lên nó.

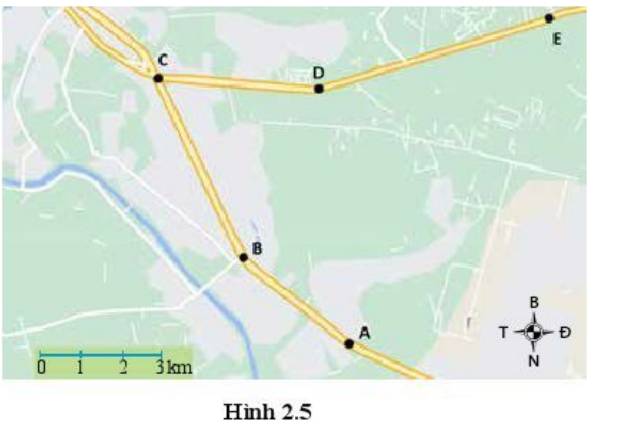
Trên bản đồ lấy điểm A là nhà, điểm E là trường học. Sử dụng một sợi chỉ kéo dài từ vị trí điểm A đến điểm E, sau đó dùng thước đo lại chiều dài của sợi chỉ rồi so với tỉ lệ của bản đồ.
Sau khi thực hiện đo và dùng tỉ lệ tương ứng trên bản đồ, ta có khoảng cách từ nhà đến trường khoảng 9 km.


Trọng lực có:
+ Điểm đặt tại trọng tâm của vật (quả táo).
+ Phương thẳng đứng.
+ Chiều từ trên xuống dưới.
+ Độ lớn phụ thuộc vào khối lượng của vật.

Quãng đường xe đi qua cổng quang điện chính là chiều rộng của tấm chắn sáng. Ta có thể dùng các dụng cụ đo độ dài như thước kẻ để đo độ rộng của tấm chắn sáng.
Trên hình 1.4, ta thấy rằng khi tấm chắn sáng bắt đầu chắn chùm tia sáng ở cổng quang điện thì đồng hồ bắt đầu đo thời gian. Ngay khi tấm chắn sáng này không chắn chùm tia sáng nữa thì đồng hồ ngừng đo. Thời gian hiện trên đồng hồ là thời gian xe đi hết quãng đường bằng chiều rộng của tấm chắn sáng. Vì vậy ta chỉ cần đo chiều rộng của tấm chắn sáng thì sẽ xác định được quãng đường xe đi qua cổng điện.

1.
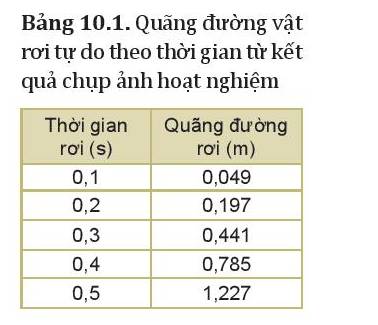
Dựa vào bảng 10.1, ta thấy rằng
+ Trong 0,1 s đầu tiên, vật đi được quãng đường là 0,049 m
+ Trong 0,1 s tiếp theo, vật đi được quãng đường là 0,197 – 0,049 = 0,148 m
+ Từ 0,2 s đến 0,3 s, vật đi được quãng đường là 0,441 – 0,197 = 0,244 m
+ Từ 0,3 s đến 0,4 s, vật đi được quãng đường là 0,785 – 0,441 = 0,344 m
+ Từ 0,4 s đến 0,5 s, vật ssi được quãng đường là 1,227 – 0,785 = 0,442 m
Thông qua các số liệu trên, ta thấy cùng trong một khoảng thời gian, quãng đường vật rơi được càng dài, chứng tỏ vật rơi tự do
2.
Gia tốc của chuyển động rơi tự do
\(a = \frac{{2s}}{{{t^2}}} = \frac{{2.0.049}}{{0,{1^2}}} = 9,8(m/{s^2})\)

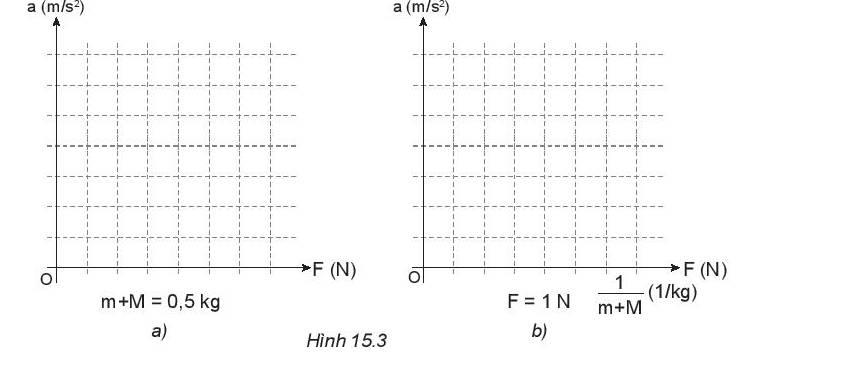
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
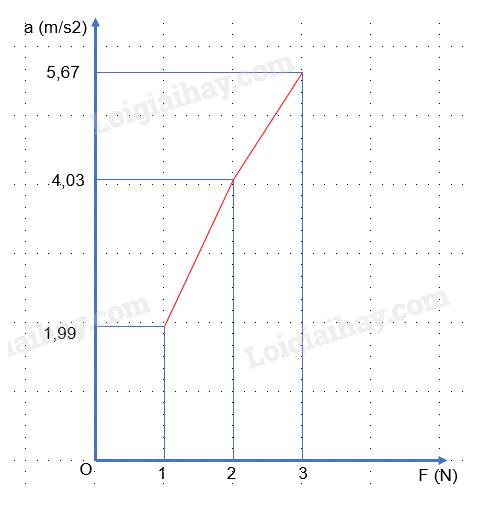
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
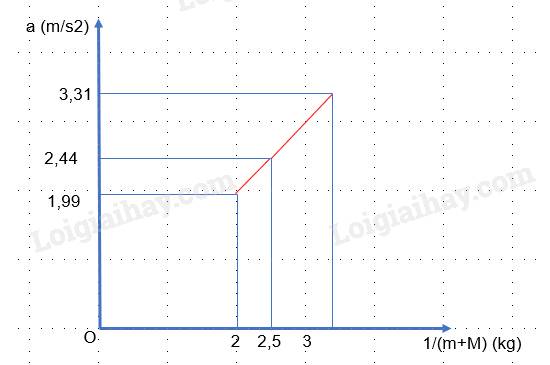
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.
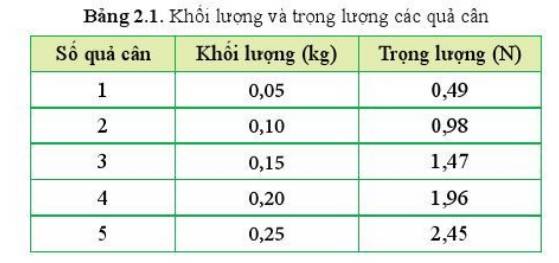




Sử dụng công thức tính trọng lực: \(P=m . g\)
Ta có:
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)