K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

9 tháng 2 2018
Vì G là trọng tâm tg ABC nên AG=2/3AA'
\(=>\frac{S_{ABG}}{S_{ABA'}}=\frac{2}{3}< =>S_{ABA'}=\frac{3}{2}S_{ABG}=\frac{3}{2}a\)
Ta có AA' là trung tuyến nên BC=2A'B
\(=>S_{ABC}=2S_{ABA'}=2.\frac{3}{2}a=3a\)
Vậy ...
HH
6 tháng 7 2020
A B C B' A' H H' M
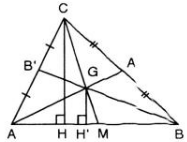
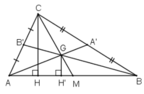
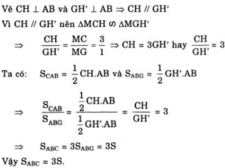
Vì \(CH\perp AB\)và \(GH'\perp AB\)=> CH // GH'
Vì \(CH//GH'\)nên \(\Delta MCH~\Delta MGH'\)
\(\Rightarrow\frac{CH}{GH'}=\frac{MC}{MG}=\frac{3}{1}=>CH=3GH'\)hay \(\frac{CH}{GH'}=3\)
Ta có : \(S_{CAB}=\frac{1}{2}CH.AB\)và \(S_{ABG}=\frac{1}{2}GH'.AB\)
\(\Rightarrow\frac{S_{CAB}}{S_{ABG}}=\frac{\frac{1}{2}CH.AB}{\frac{1}{2}GH'.AB}=\frac{CH}{GH'}=3\)
\(\Rightarrow S_{ABC}=3S_{ABG}=3S\)
Vậy : \(S_{ABC}=3S\)

SABC = 3S
vì gọi M là trung điểm AB
kẻ CH \(\perp\) AB , GK \(\perp\) AB \(\Rightarrow\) CH // GK
G là trọng tâm \(\Delta\)ABC \(\Rightarrow\) GM = \(\frac{1}{3}\) CM \(\Rightarrow\) GK = \(\frac{1}{3}\) CH \(\Rightarrow\) Đpcm
Dựng GH, CK vuông góc với AB (H, K nằm trên AB)
Ta có GH // CK
G là trọng tâm của tgiác ABC (giao của hai trung tuyến), nên đừong trung tuyến thứ 3: CC' cũng đi qua G và: C'G / C'C = 1/3
Ta có:
GH / CK = C'G / C'C = 1/3
=> CK = 3GH
=> S(ABC) = (1/2)CK.AB = (1/2).(3)GH.AB = 3.S(ABG) = 3S