Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có tam giác EPQ cân tại E và CQ là phân giác góc BCA, nên E P Q ^ = E Q P ^ = H Q C ^ = 90 0 − H C Q ^ = 90 0 − P C K ^ .
Do đó E P Q ^ + P C K ^ = 90 0 , nên P K ⊥ A C .

a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp

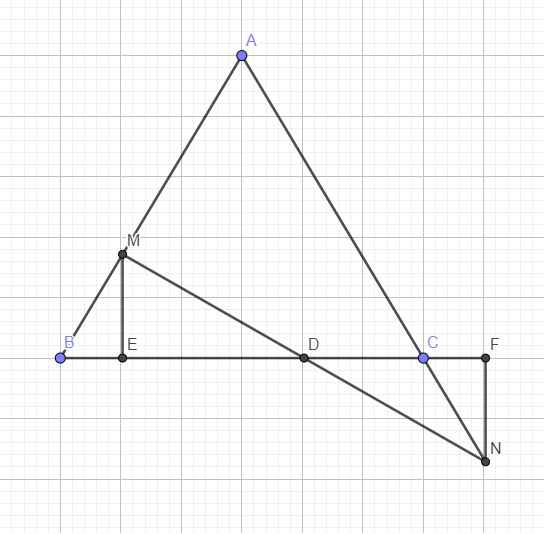
Gọi D là giao điểm MN và BC
Từ M kẻ ME vuông góc BC, từ N kẻ NF vuông góc BC
\(\widehat{B}=\widehat{C}=\widehat{NCF}\Rightarrow\Delta MBE=\Delta NCF\left(ch-gn\right)\)
\(\Rightarrow ME=NF\)
\(\Rightarrow\Delta MED=\Delta NFD\)
\(\Rightarrow MD=ND\) hay D là trung điểm MN
\(\Rightarrow D\left(-1;3\right)\Rightarrow\overrightarrow{ED}=\left(2;4\right)=2\left(1;2\right)\)
Phương trình BC (hay ED) có dạng:
\(2\left(x+3\right)-1\left(y+1\right)=0\Leftrightarrow2x-y+5=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+4=0\\2x-y+5=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;-3\right)\)
\(\Rightarrow\overrightarrow{BM}=\left(3;4\right)\) \(\Rightarrow cosB=\dfrac{\left|3.1+4.2\right|}{\sqrt{3^2+4^2}.\sqrt{1^2+2^2}}=\dfrac{11\sqrt[]{5}}{25}\)
Do C thuộc BC nên tọa độ dạng: \(C\left(c;2c+5\right)\Rightarrow\overrightarrow{NC}=\left(c+1;2c+12\right)\)
\(cosC=cosB=\dfrac{11\sqrt{5}}{25}=\dfrac{\left|1.\left(c+1\right)+2\left(2c+12\right)\right|}{\sqrt{1^2+2^2}.\sqrt{\left(c+1\right)^2+\left(2c+12\right)^2}}\)
\(\Leftrightarrow c^2+10c-96=0\Rightarrow\left[{}\begin{matrix}c=6\Rightarrow C\left(6;17\right)\\c=-16\Rightarrow C\left(-16;-27\right)\end{matrix}\right.\)
(Loại \(C\left(-16;-27\right)\) do D nằm giữa B và C)
Viết phương trình AB (qua M và B), viết phương trình AC (qua N và C). Tọa độ A là giao AB và AC

\(cosB=\dfrac{\left|1.2+\left(-7\right).1\right|}{\sqrt{1^2+\left(-7\right)^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)
Gọi vtpt của AC có tọa độ \(\left(a;b\right)\)
\(\Rightarrow cosC=cosB=\dfrac{1}{\sqrt{10}}=\dfrac{\left|2a+b\right|}{\sqrt{a^2+b^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow2\left(2a+b\right)^2=a^2+b^2\)
\(\Leftrightarrow7a^2+8ab+b^2=0\Leftrightarrow\left(a+b\right)\left(7a+b\right)=0\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}b=-1\\b=-7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;-7\right)\end{matrix}\right.\)
(Trường hợp \(\left(a;b\right)=\left(1-;7\right)\) loại do khi đó AC song song AB, vô lý)
\(\Rightarrow\) Phương trình AC: \(1\left(x-4\right)-1\left(y-0\right)=0\)