Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
\(\begin{array}{l} \Rightarrow \overrightarrow v + \overrightarrow w = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)
Và: \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)
b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)
Nên \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2})\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v = \overrightarrow v .\overrightarrow u \)

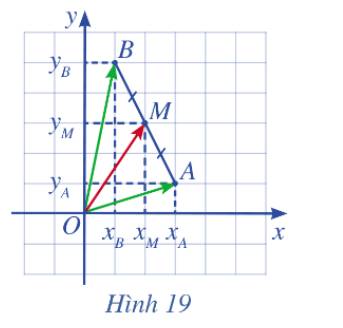
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

Để hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương thì phải tồn tại một số \(k\left( {k \in \mathbb{R}} \right)\) sao cho \(\overrightarrow u = k.\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = k{x_2}\\{y_1} = k{y_2}\end{array} \right.\) ( ĐPCM)

a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)

a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)

a) Tọa độ của vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \) là: \(\overrightarrow u + \overrightarrow v + \overrightarrow w = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)
b) Ta có: \(\overrightarrow w + \overrightarrow u = \overrightarrow v \Leftrightarrow \overrightarrow w = \overrightarrow v - \overrightarrow u \) nên \(\overrightarrow w = \left( {0 - \sqrt 3 ; - \sqrt 7 - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)

a) Vì \(\overrightarrow u = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).
Như vậy \(\overrightarrow u .\overrightarrow v = 0\)
Mặt khác: \(\overrightarrow u = \overrightarrow 0 \Leftrightarrow x = y = 0\)
\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)
b) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right)\end{array}\)
(|k|= k do k > 0)
c) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right).\end{array}\)

a) Ta có
\(\begin{array}{*{20}{l}}
{\vec a + \vec b = \left( {{a_1} + {a_2}\vec j} \right) + \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right)}\\
{\vec a - \vec b = \left( {{a_1} + {a_2}\vec j} \right) - \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} - {b_1}} \right) + \left( {{a_2} - {b_2}} \right)}\\
{k\vec a = k\left( {{a_1} + {a_2}\vec j} \right) = k{a_1} + k{a_2}\vec j}
\end{array}\)
b) Ta có
\(\begin{array}{l}
\vec a.\vec b = \left( {{a_1}\overrightarrow i + {a_2}\vec j} \right).\left( {{b_1}\overrightarrow i + {b_2}\vec j} \right)\\
= {a_1}{b_1}{\overrightarrow i ^2} + {a_1}{b_2}\overrightarrow i .\vec j + {a_2}{b_1}\overrightarrow i \vec j + {a_2}{b_2}{{\vec j}^2}\\
= {a_1}{b_1} + {a_2}{b_2}
\end{array}\)
Vì \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1,{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2} = 1,\overrightarrow i \overrightarrow j = 0\)
a) Do \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j .\), \(\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j .\)
b) +) \(\overrightarrow u + \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)
+) \(\overrightarrow u - \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)
+) \(k\overrightarrow u = \left( {k{x_1}} \right)\overrightarrow i + \left( {k{y_1}} \right)\overrightarrow j \)
c) Tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:
\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)