Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng. Giả sử A(a; b); O(0; 0) 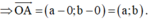
b) Đúng
c) Đúng
d) Đúng Vì tia phân giác của góc phần tư thứ nhất là đường thẳng y = x.

a) Sai
Sửa lại: Điểm A nằm trên trục hoành thì có tung độ bằng 0.
b) Sai
Ví dụ: A(2; 6), B(–4; 0) có trung bình cộng các hoành độ bằng –1.
P(–1; 3) là trung điểm của AB
P(–1; 2) không phải trung điểm của AB
P(–1; 0) không phải trung điểm của AB.
c) Đúng
ABCD là hình bình hành nên giao điểm O của AC và BD đồng thời là trung điểm của AC và BD
O là trung điểm của AC 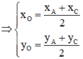
O là trung điểm của BD 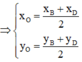
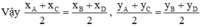

a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)
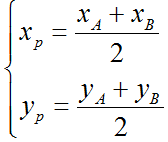
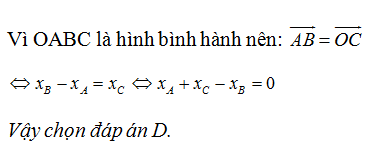
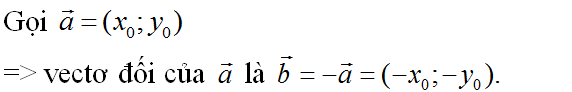
Các câu a, b, c đúng; d sai